题目内容
14．与函数f（x）=$\sqrt{{x}^{2}}$表示同一函数提（ ）| A． | g（x）=$\frac{{x}^{2}}{x}$ | B． | g（x）=（$\sqrt{x}$）2 | C． | g（x）=x | D． | g（x）=|x| |
分析 根据两个函数的定义域相同，对应关系也相同，即可判断它们是同一函数．
解答 解：对于A，g（x）=$\frac{{x}^{2}}{x}$=x的定义域是{x|x≠0}，f（x）=$\sqrt{{x}^{2}}$=|x|的定义域是R，定义域不同，对应关系也不同，不是同一函数；
对于B，g（x）=${（\sqrt{x}）}^{2}$=x的定义域是{x|x≥0}，f（x）=$\sqrt{{x}^{2}}$=|x|的定义域是R，定义域不同，对应关系也不同，不是同一函数；
对于C，g（x）=x的定义域是R，f（x）=$\sqrt{{x}^{2}}$=|x|的定义域是R，对应关系不同，不是同一函数；
对于D，g（x）=|x|的定义域是R，f（x）=$\sqrt{{x}^{2}}$=|x|的定义域是R，定义域相同，对应关系也相同，是同一函数．
故选：D．
点评 本题考查了判断两个函数为同一函数的应用问题，是基础题目．
练习册系列答案
相关题目
9．某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的所有数据．
B地区用户满意度评分：92，60，69，70，76，82，70，85，72，87，67，50，91，96，70，82，94，85，75，59，74，89，77，88，78，67，79，94，78，65，64，73，60，75，86，65，90，84，74，80
（1）完成B地区用户满意度评分的频率分布表并作出频率分布直方图；
B地区用户满意度评分的频率分布表
（2）通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）；
（3）根据用户满意度评分，将用户的满意度分为三个等级：
利用样本近似估计总体的思想方法，估计哪个地区用户的满意度等级为不满意的概率大？说明理由．
B地区用户满意度评分：92，60，69，70，76，82，70，85，72，87，67，50，91，96，70，82，94，85，75，59，74，89，77，88，78，67，79，94，78，65，64，73，60，75，86，65，90，84，74，80
（1）完成B地区用户满意度评分的频率分布表并作出频率分布直方图；
B地区用户满意度评分的频率分布表
| 满意度评分分组 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100） |
| 频数 | |||||
| 频率 |
（2）通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）；
（3）根据用户满意度评分，将用户的满意度分为三个等级：
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
6．在△ABC中，若A=$\frac{π}{3}$，b=16，此三角形面积S=220$\sqrt{3}$，则a的值是（ ）
| A． | $20\sqrt{6}$ | B． | 75 | C． | 51 | D． | 49 |
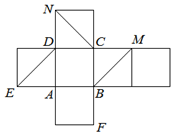如图是正方体的平面展开图．在这个正方体中，