如图是正方体的平面展开图．在这个正方体中.①BM与ED是异面直线,②CN与BE平行,③CN与BM成60°角,④DM与BN垂直．以上四个命题中.正确命题的序号是( )A．①②③④B．②④C．②③④D．②③ 题目和参考答案——青夏教育精英家教网—

题目内容

3．

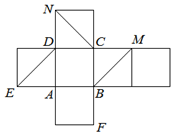如图是正方体的平面展开图．在这个正方体中，
①BM与ED是异面直线；
②CN与BE平行；
③CN与BM成60°角；
④DM与BN垂直．
以上四个命题中，正确命题的序号是（　　）

A．

①②③④

B．

②④

C．

②③④

D．

②③

分析由已知中的正方体平面展开图，画出正方体的直观图，结合正方体的几何特征，判断题目中的命题即可．

解答解：由已知正方体的平面展开图，得到正方体的直观图，如图所示：
由正方体的几何特征得：
①BM与ED是相对两个平行平面的两条异面的对角线，∴①正确；
②CN与BE是相对两个平行平面的两条平行的对角线，∴②正确；
③CN与AF是相对两个平行平面的两条异面垂直的对角线，∴③正确；
④DM⊥平面BCN，所以④正确；
综上，正确的命题是①②③④；
故选：A．

点评本题考查了根据已知中的正方体平面展开图，得到正方体的直观图，是易错题．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

14．与函数f（x）=$\sqrt{{x}^{2}}$表示同一函数提（　　）

A．

g（x）=$\frac{{x}^{2}}{x}$

11．某汽车美容公司为吸引顾客，推出优惠活动：对首次消费的顾客，按200元/次收费，并注册成为会员，对会员逐次消费给予相应优惠，标准如表：

消费次第	第1次	第2次	第3次	第4次	≥5次
收费比例	1	0.95	0.90	0.85	0.80

该公司从注册的会员中，随机抽取了100位进行统计，得到统计数据如表：

消费次第	第1次	第2次	第3次	第4次	第5次
频数	60	20	10	5	5

假设汽车美容一次，公司成本为150元，根据所给数据，解答下列问题：
（1）估计该公司一位会员至少消费两次的概率；
（2）某会员仅消费两次，求这两次消费中，公司获得的平均利润；
（3）以事件发生的频率作为相应事件发生的概率，设该公司为一位会员服务的平均利润为X元，求X的分布列和数学期望E（X）．

18．函数y=lg（1-x）+lg（1+x）是（　　）

	A．	奇函数，且在（0，1）上是增函数		B．	奇函数，且在（0，1）上是减函数
	C．	偶函数，且在（0，1）上是增函数		D．	偶函数，且在（0，1）上是减函数

8．在一次考试中，某班学生的及格率是70%，这里所说的70%是频率（填概率或频率）

15．（1班、3班做）已知函数f（x）=-$\frac{π}{12x}$，g（x）=xcosx-sinx，当x∈[-3π，3π]时，方程f（x）=g（x）的根的个数是（　　）

12．已知函数f（x）=2sin xcos x-2sin²x+1（x∈R），若在△ABC中，内角A，B，C的对边分别为a，b，c，a=$\sqrt{3}$，A为锐角，且f（A+$\frac{π}{8}$）=$\frac{{\sqrt{2}}}{3}$，则△ABC面积的最大值为（　　）

A．

$\frac{{3（\sqrt{3}+\sqrt{2}）}}{4}$

B．

$\frac{\sqrt{3}}{4}$

C．