题目内容
已知: =(x,4,1),
=(x,4,1), =(-2,y,-1),
=(-2,y,-1), =(3,-2,z),
=(3,-2,z), ∥
∥ ,
, ⊥
⊥ ,求:
,求:
(1) ,
, ,
, ;
;
(2)( +
+ )与(
)与( +
+ )所成角的余弦值.
)所成角的余弦值.
解:(1)∵ ,∴
,∴ ,解得x=2,y=-4,
,解得x=2,y=-4,
故 =(2,4,1),
=(2,4,1), =(-2,-4,-1),
=(-2,-4,-1),
又因为 ,所以
,所以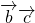 =0,即-6+8-z=0,解得z=2,
=0,即-6+8-z=0,解得z=2,
故 =(3,-2,2)
=(3,-2,2)
(2)由(1)可得 =(5,2,3),
=(5,2,3), =(1,-6,1),
=(1,-6,1),
设向量 与
与 所成的角为θ,
所成的角为θ,
则cosθ= =
=
分析:(1)由向量的平行和垂直可得关于xyz的关系式,解之即可得向量坐标;
(2)由(1)可得向量 与
与 的坐标,进而由夹角公式可得结论.
的坐标,进而由夹角公式可得结论.
点评:本题考查空间向量平行和垂直的判断,涉及向量的夹角公式,属基础题.
 ,∴
,∴ ,解得x=2,y=-4,
,解得x=2,y=-4,故
 =(2,4,1),
=(2,4,1), =(-2,-4,-1),
=(-2,-4,-1),又因为
 ,所以
,所以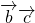 =0,即-6+8-z=0,解得z=2,
=0,即-6+8-z=0,解得z=2,故
 =(3,-2,2)
=(3,-2,2)(2)由(1)可得
 =(5,2,3),
=(5,2,3), =(1,-6,1),
=(1,-6,1),设向量
 与
与 所成的角为θ,
所成的角为θ,则cosθ=
 =
=
分析:(1)由向量的平行和垂直可得关于xyz的关系式,解之即可得向量坐标;
(2)由(1)可得向量
 与
与 的坐标,进而由夹角公式可得结论.
的坐标,进而由夹角公式可得结论.点评:本题考查空间向量平行和垂直的判断,涉及向量的夹角公式,属基础题.

练习册系列答案
相关题目