题目内容
已知以 为首项的数列
为首项的数列 满足:
满足:
(1)若 ,求证:
,求证: ;
;
(2)若 ,求使
,求使 对任意正整数n都成立的
对任意正整数n都成立的 与
与 .
.
(1)证明过程详见解析;(2)当 时,满足题意的
时,满足题意的 N*; 当
N*; 当 时,满足题意的
时,满足题意的 N*.
N*.
解析试题分析:本题考查数列与函数的综合知识.第一问,将 从3断开,分成两部分,分别求出
从3断开,分成两部分,分别求出 的范围;第二问,分别验证每一种情况.
的范围;第二问,分别验证每一种情况.
试题解析:(1)当 时,则
时,则
 ,当
,当 时,则
时,则 ,
,
故 ,所以当
,所以当 时,总有
时,总有 . 8分
. 8分
(2)①当 时,
时, ,故满足题意的
,故满足题意的 .
.
同理可得,当 或4时,满足题意的
或4时,满足题意的 N*.
N*.
当 或6时,满足题意的
或6时,满足题意的 N*.
N*.
②当 时,
时, ,故满足题意的k不存在.
,故满足题意的k不存在.
③当 时,由(1)知,满足题意的k不存在.
时,由(1)知,满足题意的k不存在.
综上得:当 时,满足题意的
时,满足题意的 N*;
N*;
当 时,满足题意的
时,满足题意的 N*. 16分.
N*. 16分.
考点:1.求分段函数的值域;2.恒成立问题;3.分类讨论思想.

练习册系列答案
相关题目
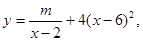 其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数) 的表达式;
的表达式;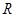 上的函数
上的函数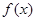 对任意
对任意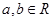 都有
都有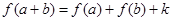 (
(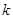 为常数).
为常数).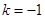 ,
,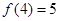 ,若不等式
,若不等式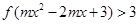 对任意
对任意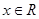 恒成立,求实数
恒成立,求实数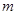 的取值范围.
的取值范围.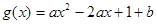 (
(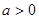 )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 ,
,  、
、 的值;
的值; 在
在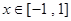 上有解,求实数
上有解,求实数 的取值范围.
的取值范围. (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式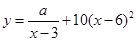 ,其中
,其中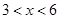 ,
, 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.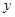 万元与投入
万元与投入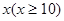 万元之间满足:
万元之间满足: 为常数。当
为常数。当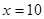 万元时,
万元时,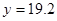 万元;
万元;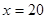 万元时,
万元时,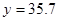 万元。 (参考数据:
万元。 (参考数据: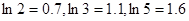 )
) 的解析式;
的解析式; 的最大值。(利润=旅游增加值-投入)。
的最大值。(利润=旅游增加值-投入)。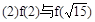
 .
. 的单调区间;
的单调区间;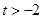 时,判断
时,判断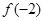 和
和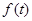 的大小,并说明理由;
的大小,并说明理由;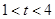 时,关于
时,关于 的方程:
的方程: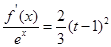 在区间
在区间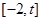 上总有两个不同的解.
上总有两个不同的解.