题目内容
我省某景区为提高经济效益,现对某一景点进行改造升级,从而扩大内需,提高旅游增加值,经过市场调查,旅游增加值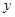 万元与投入
万元与投入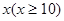 万元之间满足:
万元之间满足: 为常数。当
为常数。当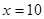 万元时,
万元时,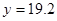 万元;
万元;
当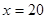 万元时,
万元时,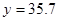 万元。 (参考数据:
万元。 (参考数据: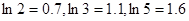 )
)
(1)求 的解析式;
的解析式;
(2)求该景点改造升级后旅游利润 的最大值。(利润=旅游增加值-投入)。
的最大值。(利润=旅游增加值-投入)。
(1)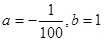 (2)24.4万元.
(2)24.4万元.
解析试题分析:(1)用待定系数法,把给定的两组数据代入函数解析式联立方程组解出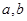 的值即可.(2)首先用导数知识判断函数的单调性,从而求出极大值点,进而求得最大值.
的值即可.(2)首先用导数知识判断函数的单调性,从而求出极大值点,进而求得最大值.
试题解析:(1)由条件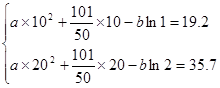 2分
2分
解得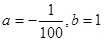 4分
4分
则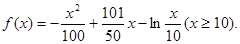 6分
6分
(2)由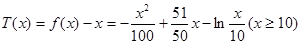
则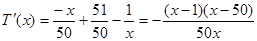 9分
9分
令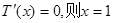 (舍)或
(舍)或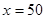
当 时,
时,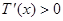 ,因此
,因此 在(10,50)上是增函数;
在(10,50)上是增函数;
当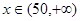 时,
时,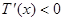 ,因此
,因此 在(0,+∞)上是减函数,
在(0,+∞)上是减函数,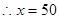 为
为 的极大值点 11分
的极大值点 11分
即该景点改造升级后旅游利润
 )的最大值为
)的最大值为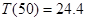 万元。 12分
万元。 12分
考点:函数的实际应用,待定系数法求函数解析式,函数的单调性和极值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数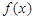 的定义域为
的定义域为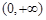 ,若
,若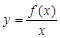 在
在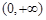 上为增函数,则称
上为增函数,则称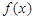 为“一阶比增函数”;若
为“一阶比增函数”;若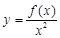 在
在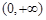 上为增函数,则称
上为增函数,则称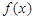 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为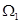 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为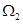 .
.
(Ⅰ)已知函数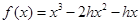 ,若
,若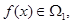 且
且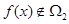 ,求实数
,求实数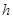 的取值范围;
的取值范围;
(Ⅱ)已知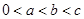 ,
,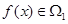 且
且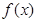 的部分函数值由下表给出,
的部分函数值由下表给出,
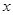 |  | 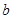 | 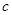 |  |
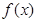 | 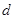 | 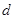 | 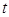 | 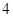 |
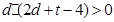 ;
;(Ⅲ)定义集合

请问:是否存在常数
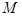 ,使得
,使得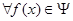 ,
,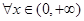 ,有
,有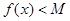 成立?若存在,求出
成立?若存在,求出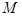 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由. 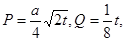 其中
其中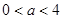 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),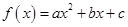 .
.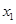 、
、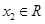 ,且
,且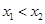 ,都有
,都有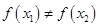 ,求证:关于
,求证:关于 的方程
的方程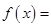
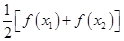 有两个不相等的实数根且必有一个根属于
有两个不相等的实数根且必有一个根属于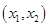 ;
;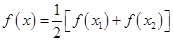 在
在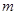 ,且
,且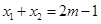 ,设函数
,设函数 的图象的对称轴方程为
的图象的对称轴方程为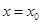 ,求证:
,求证: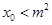 .
. 为首项的数列
为首项的数列 满足:
满足:
 ,求证:
,求证: ;
;  ,求使
,求使 对任意正整数n都成立的
对任意正整数n都成立的 与
与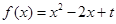 与两坐标轴分别交于不同的三点A、B、C.
与两坐标轴分别交于不同的三点A、B、C.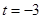 时,求经过A、B、C三点的圆F的方程;
时,求经过A、B、C三点的圆F的方程;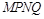 的面积的最大值。
的面积的最大值。 .
. 的单调区间;
的单调区间; ,
, 总成立,求实数
总成立,求实数 的取值范围;
的取值范围; ,
, . 过点
. 过点 作函数
作函数 图像的所有切线,令各切点的横坐标构成数列
图像的所有切线,令各切点的横坐标构成数列 ,求数列
,求数列 的值.
的值. ,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2.
,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2.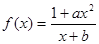
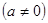 是奇函数,并且函数
是奇函数,并且函数 的图像经过点(1,3).
的图像经过点(1,3). 的值;
的值;