题目内容
已知△ABC为等边三角形, ,设点P,Q满足
,设点P,Q满足 ,
, ,
, ,若
,若 ,则
,则 ( )
( )
A. | B. | C.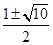 | D. |
A
解析试题分析:如图所示,
∵ =[(1-λ)
=[(1-λ)
=(λ-λ2+1)
 =22cos60°=2,
=22cos60°=2, ,
,
∴ =2(λ-λ2+1)-4(1-λ)-4λ=2λ-2λ2-2,
=2(λ-λ2+1)-4(1-λ)-4λ=2λ-2λ2-2,
又∵ ,
,
∴2λ-2λ2-2=- ,化为(2λ-1)2=0,解得λ=
,化为(2λ-1)2=0,解得λ= .故选A。
.故选A。
考点:本题主要考查平面向量的线性运算,数量积。
点评:典型题,涉及平面向量线性运算问题往往要注意结合图形,应用三角形法则或平行四边形法则,完成线性运算。向量的数量积注意有定义式、坐标运算。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设向量 ,
, ,若满足
,若满足 ,则
,则 ( )
( )
A. | B. | C. | D. |
点
 共面,若
共面,若 ,则
,则 的面积与
的面积与 的面积之比为( )
的面积之比为( )
A. | B. | C. | D. |
已知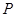 是
是 所在平面内一点,
所在平面内一点,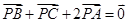 ,现将一粒红豆随机撒在
,现将一粒红豆随机撒在 内,则红豆落在
内,则红豆落在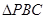 内的概率是( )
内的概率是( )
A.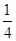 | B.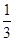 | C.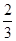 | D.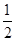 |
已知A(a,0),B(0,a)(a>0), =t
=t ,O为坐标原点,则|
,O为坐标原点,则| |的最小值为( )
|的最小值为( )
A. a a | B. a a | C. a a | D.a |
设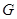 为△
为△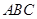 的重心,且
的重心,且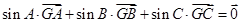 ,则
,则 的大小为( )
的大小为( )
| A.450 | B.600 | C.300 | D.150 |
已知 与
与 为互相垂直的单位向量,
为互相垂直的单位向量,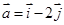 ,
, 且
且 与
与 的夹角为锐角,则实数
的夹角为锐角,则实数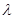 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
如右图所示,已知 是等腰直角三角形,
是等腰直角三角形, ,
, 则
则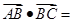 (***)
(***)
| A.4 | B. | C.2 | D.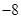 |
设向量 满足
满足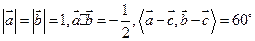 ,则
,则 的最大值等于
的最大值等于
| A.2 | B.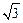 | C. | D.1 |