题目内容
设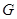 为△
为△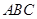 的重心,且
的重心,且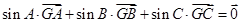 ,则
,则 的大小为( )
的大小为( )
| A.450 | B.600 | C.300 | D.150 |
B
解析试题分析:∵G是三角形ABC的重心,∴ ,则
,则 ,代入
,代入 得,
得,
(sinB-sinA) +(sinC-sinA)
+(sinC-sinA) =
= ,
,
∵ ,
, 不共线,∴sinB-sinA=0,sinC-sinA=0,
不共线,∴sinB-sinA=0,sinC-sinA=0,
则sinB=sinA=sinC,根据正弦定理知:b=a=c,
∴三角形是等边三角形,则角B=60°.
故选B.
考点:本题主要考查三角形的重心,平面向量的线性运算及向量共线的条件,正弦定理。
点评:中档题,利用三角形重心对应的向量条件的应用,把几何问题转化为向量问题,根据条件和正弦定理判断出三角形的形状。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知直线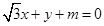 与圆
与圆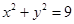 交于
交于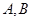 两点,则与向量
两点,则与向量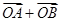 (
(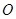 为坐标原点)共线的一个向量为( )
为坐标原点)共线的一个向量为( )
A.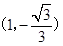 | B.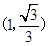 | C.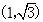 | D.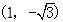 |
设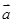 、
、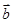 都是非零向量,下列四个条件中,一定能使
都是非零向量,下列四个条件中,一定能使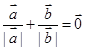 成立的是( )
成立的是( )
A.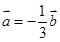 | B. | C.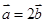 | D.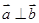 |
设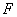 为抛物线
为抛物线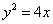 的焦点,
的焦点, 、
、 、
、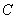 为该抛物线上三点,若
为该抛物线上三点,若 ,则
,则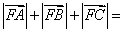 ( )
( )
| A.9 | B.6 | C.4 | D.3 |
已知△ABC为等边三角形, ,设点P,Q满足
,设点P,Q满足 ,
, ,
, ,若
,若 ,则
,则 ( )
( )
A. | B. | C.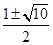 | D. |
若平面向量a=(1,x)和b=(2x+3,-x)互相平行,其中x∈R,
则|a-b|=( )
A. | B.2或 | C.-2或0 | D.2或10 |
设点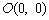 、
、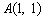 、
、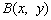 且
且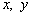 满足
满足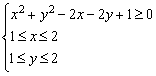 ,则
,则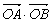 取得最小值时,点B的个数是( )
取得最小值时,点B的个数是( )
| A.1个 | B.2个 | C.3个 | D.无数个 |
已知向量 ,
, ,若
,若 ,则实数x的值为
,则实数x的值为
| A.1 | B. | C. | D. |
 的外接圆的圆心为O,半径为1,
的外接圆的圆心为O,半径为1, ,
, 且
且 ,则向量
,则向量 在向量
在向量 方向上的投影为( )
方向上的投影为( )
A.  | B. | C. | D. |