题目内容
【题目】若不等式|2x﹣1|﹣|x+a|≥a对任意的实数x恒成立,则实数a的取值范围是( )
A.(﹣∞,﹣ ![]() ]
]
B.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
C.(﹣ ![]() ,0)
,0)
D.(﹣∞,﹣ ![]() ]
]
【答案】D
【解析】解:﹣a< ![]() 时,|2x﹣1|﹣|x+a|=
时,|2x﹣1|﹣|x+a|= 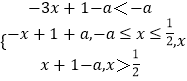 ,x=
,x= ![]() 时,最小值为﹣
时,最小值为﹣ ![]() ﹣a,
﹣a,
∵不等式|2x﹣1|﹣|x+a|≥a对任意的实数x恒成立,
∴﹣ ![]() ﹣a≥a,∴a≤﹣
﹣a≥a,∴a≤﹣ ![]() ,
,
∴﹣ ![]() <a≤﹣
<a≤﹣ ![]() ;
;
﹣a= ![]() 时,|2x﹣1|﹣|x+a|=|x﹣
时,|2x﹣1|﹣|x+a|=|x﹣ ![]() |≥﹣
|≥﹣ ![]() ,成立;
,成立;
﹣a> ![]() 时,同理可得x=
时,同理可得x= ![]() 时,|2x﹣1|﹣|x+a|最小值为
时,|2x﹣1|﹣|x+a|最小值为 ![]() +a,
+a,
∵不等式|2x﹣1|﹣|x+a|≥a对任意的实数x恒成立,
∴ ![]() +a≥a恒成立,∴a<﹣
+a≥a恒成立,∴a<﹣ ![]() .
.
综上所述a≤﹣ ![]() .
.
故选D.

练习册系列答案
相关题目
【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如下表:
x |
|
|
|
|
|
|
|
y | ﹣1 | 1 | 3 | 1 | ﹣1 | 1 | 3 |
(1)根据表格提供的数据求函数f(x)的一个解析式.
(2)根据(1)的结果,若函数y=f(kx)(k>0)周期为 ![]() ,当
,当 ![]() 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.