Question

【题目】已知x∈R，[x]表示不超过x的最大整数，若函数 有且仅有3个零点，则实数a的取值范围是．

Answer 1

【答案】
【解析】解：由 得 =2a， ①若x＞0，设g（x）= ，
则当0＜x＜1，[x]=0，此时g（x）=0，
当1≤x＜2，[x]=1，此时g（x）= ，此时 ＜g（x）≤1，
当2≤x＜3，[x]=2，此时g（x）= ，此时 ＜g（x）≤1，
当3≤x＜4，[x]=3，此时g（x）= ，此时 ＜g（x）≤1，
当4≤x＜5，[x]=4，此时g（x）= ，此时 ＜g（x）≤1，
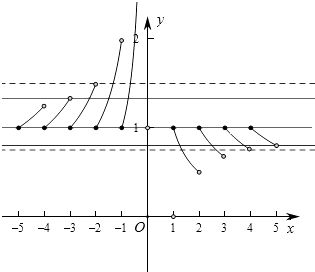
作出函数g（x）的图象，
要使 有且仅有三个零点，
即函数g（x）=2a有且仅有三个零点，
则由图象可知 ＜a≤ ，
②若x＜0，设g（x）= ，
则当﹣1≤x＜0，[x]=﹣1，此时g（x）=﹣ ，此时g（x）≥1，
当﹣2≤x＜﹣1，[x]=﹣2，此时g（x）=﹣ ，此时1≤g（x）＜2，
当﹣3≤x＜﹣2，[x]=﹣3，此时g（x）=﹣ ，此时1≤g（x）＜ ，
当﹣4≤x＜﹣3，[x]=﹣4，此时g（x）=﹣ ，此时1≤g（x）＜ ，
当﹣5≤x＜﹣4，[x]=﹣5，此时g（x）=﹣ ，此时1≤g（x）＜ ，
作出函数g（x）的图象，
要使 有且仅有三个零点，
即函数g（x）=2a有且仅有三个零点，
则由图象可知 ≤a＜ ，
综上： ＜a≤ 或 ≤a＜ ，
所以答案是： ．

【考点精析】解答此题的关键在于理解函数的零点与方程根的关系的相关知识，掌握二次函数的零点：（1）△＞0，方程 有两不等实根，二次函数的图象与 轴有两个交点，二次函数有两个零点;（2）△＝0，方程 有两相等实根（二重根），二次函数的图象与 轴有一个交点，二次函数有一个二重零点或二阶零点;（3）△＜0，方程 无实根，二次函数的图象与 轴无交点，二次函数无零点．