Question

【题目】（本小题满分12分，（1）小问5分，（2）小问7分）

如图，椭圆的左、右焦点分别为过的直线交椭圆于两点，且

（1）若，求椭圆的标准方程

（2）若求椭圆的离心率

Answer 1

【答案】（1）；（2）

【解析】

试题解析：（1）本题中已知椭圆上的一点到两焦点的距离，因此由椭圆定义可得长轴长，即参数的值，而由，应用勾股定理可得焦距，即的值，因此方程易得；（2）要求椭圆的离心率，就是要找到关于的一个等式，题中涉及到焦点距离，因此我们仍然应用椭圆定义，设，则，，于是有，这样在中求得，在中可建立关于的等式，从而求得离心率.

（1）由椭圆的定义，

设椭圆的半焦距为c，由已知，因此

即

从而

故所求椭圆的标准方程为.

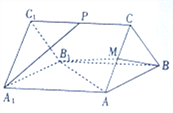
（2）解法一：如图（21）图，设点P在椭圆上，且，则

求得

由,得,从而

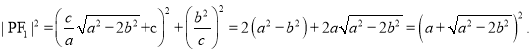
由椭圆的定义，,从而由，有

又由，知，因此

于是

解得.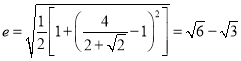

解法二：如图由椭圆的定义，,从而由，有

又由，知，因此,

,从而

由,知，因此