题目内容
已知x+y=xy,x>0,y>0则x+y的最小值是________.
4
分析:由 ≤
≤ 将方程转化为不等式,利用换元法和二次不等式的解法求出“x+y”的范围,即求出它的最小值.
将方程转化为不等式,利用换元法和二次不等式的解法求出“x+y”的范围,即求出它的最小值.
解答:∵x>0,y>0,∴ ≤
≤ (当且仅当x=y时取等号),
(当且仅当x=y时取等号),
则xy≤ ,
,
∵xy=(x+y)≤ ,
,
设t=x+y,则t>0,代入上式得,t2-4t≥0,
解得,t≥4,
故x+y的最小值是4,
故答案为:4.
点评:本题考查了基本不等式的应用,还涉及了二次不等式的解法、换元法,利用换元法时一定注意换元后的范围,考查了转化思想和整体思想.
分析:由
 ≤
≤ 将方程转化为不等式,利用换元法和二次不等式的解法求出“x+y”的范围,即求出它的最小值.
将方程转化为不等式,利用换元法和二次不等式的解法求出“x+y”的范围,即求出它的最小值.解答:∵x>0,y>0,∴
 ≤
≤ (当且仅当x=y时取等号),
(当且仅当x=y时取等号),则xy≤
 ,
,∵xy=(x+y)≤
 ,
,设t=x+y,则t>0,代入上式得,t2-4t≥0,
解得,t≥4,
故x+y的最小值是4,
故答案为:4.
点评:本题考查了基本不等式的应用,还涉及了二次不等式的解法、换元法,利用换元法时一定注意换元后的范围,考查了转化思想和整体思想.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
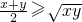 ;
;