题目内容
16.已知数列{an}的前n项和为Sn,且满足a1=-2,an+1+3Sn+2=0(n∈N*).(1)求a2、a3的值;
(2)求数列{an}的通项公式;
(3)是否存在整数对(m、n),使得等式an2-m•an=4m+8成立?若存在,请求出所有满足条件的(m,n);若不存在,请说明理由.
分析 (1)根据递推公式即可求出a2、a3的值;
(2)an+1+3Sn+2=0,①,an+2+3Sn+1+2=0,②,得到an+2=-2an+1,继而得到数列{an}是以-2为首项,以-2为公比的等比数列,问题得以解决;
(3)由题意求出m=(-2)n-4+$\frac{8}{(-2)^{n}+4}$,分别代入n的值求出(m,n)的坐标.
解答 解:(1)a1=-2,an+1+3Sn+2=0(n∈N*),
∴a2+3S1+2=0,a3+3S2+2=0,
∴a2+3a1+2=0,a3+3(a1+a2)+2=0,
∴a2=4,a3=-8,
(2)an+1+3Sn+2=0,①,
an+2+3Sn+1+2=0,②,
②-①得,an+2-an+1+3(Sn+1+Sn)=0,
∴an+2=-2an+1,
∴$\frac{{a}_{n+2}}{{a}_{n+1}}$=-2,
∴数列{an}是以-2为首项,以-2为公比的等比数列,
∴an=-2×(-2)n-1=(-2)n,
(3)∵an2-m•an=4m+8,
∴m=$\frac{{{a}_{n}}^{2}-8}{4+{a}_{n}}$=$\frac{(-2)^{2n}-8}{(-2)^{n}+4}$=$\frac{(-2)^{2n}-16+8}{(-2)^{n}+4}$=(-2)n-4+$\frac{8}{(-2)^{n}+4}$,
∵m为整数,则$\frac{8}{(-2)^{n}+4}$为整数,
当n=1时,m=-2,
当n=2时,m=1,
当n=3时,m=-14,
则满足条件的(m,n)共有(-2,1),(1,2),(-14,3).
点评 本题考查了数列的递推公式,等比数列的通项公式,考查了学生的运算能力,属于中档题.

练习册系列答案
相关题目
6.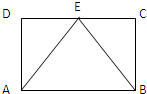 如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )
如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )
 如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )
如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
4.圆x2+y2=9与圆(x-1)2+(y+1)2=16的位置关系是( )
| A. | 相交 | B. | 内切 | C. | 外切 | D. | 相离 |
11.与直线x+2y-4=0在x轴上的截距相同,与直线xtan$\frac{2π}{3}$+y-4=0的倾斜角相同的直线方程为( )
| A. | $\sqrt{3}$x-y-4=0 | B. | $\sqrt{3}$x-y-4$\sqrt{3}$=0 | C. | $\sqrt{3}$x+y-4=0 | D. | $\sqrt{3}$x+y-4$\sqrt{3}$=0 |