题目内容
(理)已知对于任意正整数n,都有a1+a2+…+an=n3,则
(
+
+…+
)=______.
| lim |
| n→+∞ |
| 1 |
| a2-1 |
| 1 |
| a3-1 |
| 1 |
| an-1 |
∵当n≥2时,有a1+a2+…+an-1+an=n3,
a1+a2+…+an-1=(n-1)3,
两式相减,得an=3n2-3n+1,
∴
=
=
(
-
),
∴
+
+…+
,
=
(1-
)+
(
-
)+…+
(
-
),
=
(1-
).
∴
(
+
+…+
)
=
(1-
)
=
.
故答案为:
.
a1+a2+…+an-1=(n-1)3,
两式相减,得an=3n2-3n+1,
∴
| 1 |
| an-1 |
| 1 |
| 3n(n-1) |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
∴
| 1 |
| a2-1 |
| 1 |
| a3-1 |
| 1 |
| an-1 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
=
| 1 |
| 3 |
| 1 |
| n |
∴
| lim |
| n→+∞ |
| 1 |
| a2-1 |
| 1 |
| a3-1 |
| 1 |
| an-1 |
=
| lim |
| n→∞ |
| 1 |
| 3 |
| 1 |
| n |
=
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
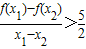 ;
;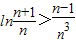 恒成立.
恒成立. = .
= .