题目内容
(理)已知对于任意正整数n,都有a1+a2+…+an=n3,则 = .
= .
【答案】分析:先根据n≥2时,a1+a2+…+an-1+an=n3,a1+a2+…+an-1=(n-1)3,把两式相减,得出an的表达式,再根据  =
= (
(  -
- )进行解答即可.
)进行解答即可.
解答:解:∵当n≥2时,有a1+a2+…+an-1+an=n3,
a1+a2+…+an-1=(n-1)3,
两式相减,得an=3n2-3n+1,
∴ =
= =
= (
(  -
- ),
),
∴ +
+ +…+
+…+ ,
,
= (1-
(1- )+
)+ (
(  -
- )+…+
)+…+ (
(  ),
),
= (1-
(1- ).
).
∴
=
= .
.
故答案为: .
.
点评:本题考查的是部分分式,属规律性题目,能根据题意得出 =
= (
(  -
- )是解答此题的关键.
)是解答此题的关键.
 =
= (
(  -
- )进行解答即可.
)进行解答即可.解答:解:∵当n≥2时,有a1+a2+…+an-1+an=n3,
a1+a2+…+an-1=(n-1)3,
两式相减,得an=3n2-3n+1,
∴
 =
= =
= (
(  -
- ),
),∴
 +
+ +…+
+…+ ,
,=
 (1-
(1- )+
)+ (
(  -
- )+…+
)+…+ (
(  ),
),=
 (1-
(1- ).
).∴

=

=
 .
.故答案为:
 .
.点评:本题考查的是部分分式,属规律性题目,能根据题意得出
 =
= (
(  -
- )是解答此题的关键.
)是解答此题的关键. 
练习册系列答案
相关题目
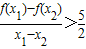 ;
;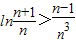 恒成立.
恒成立.