��Ŀ����
����Ŀ������С������14�֣���
ij�߲˻�����ֲ���������������г������֪���Ӷ���һ�����300���ڣ����������ۼ�������ʱ��Ĺ�ϵ��ͼһ��һ�����߱�ʾ������������ֲ�ɱ�������ʱ��Ĺ�ϵ��ͼ���������߶α�ʾ��
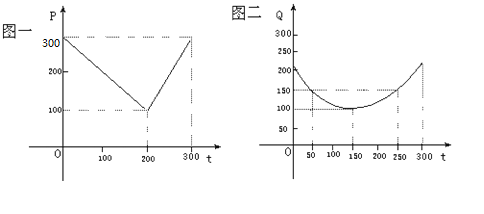
������д��ͼһ��ʾ���г��ۼ���ʱ��ĺ�����ϵʽ![]() ��д��ͼ����ʾ����ֲ�ɱ�������ʱ��ĺ�����ϵʽ
��д��ͼ����ʾ����ֲ�ɱ�������ʱ��ĺ�����ϵʽ![]() ��
��
�����������趨�г��ۼۼ�ȥ��ֲ�ɱ�Ϊ�����棬�ʺ�ʱ���е����������������ע���г��ۼۺ���ֲ�ɱ��ĵ�λ��Ԫ/102�K��ʱ�䵥λ���죩
���𰸡���1��![]()
![]()
��2���Ӷ���һ�տ�ʼ�ĵ�50��ʱ�����е����������������
��������
��������������Ǻ���Ӧ���⣬��1��������ϵʽ��ʽ�����Ѿ�������![]() �Ƿֹ�������ͼ���������߶Σ�һ�κ�������ʽ���ֱ�������ɣ�
�Ƿֹ�������ͼ���������߶Σ�һ�κ�������ʽ���ֱ�������ɣ�![]() �������ߣ����κ���������ʽ����Ϊһ��ʽ��ʽ����2���ɣ�1���ɵô�����
�������ߣ����κ���������ʽ����Ϊһ��ʽ��ʽ����2���ɣ�1���ɵô�����![]() �����Ƿֶκ����������ֵҪ�ֶ��������ȡ����һ����
�����Ƿֶκ����������ֵҪ�ֶ��������ȡ����һ����
�����������1����ͼ1�ɵ��г��ۼ���ʱ��ĺ�����ϵΪ![]()
��ͼ2�ɵ���ֲ�ɱ���ʱ��ĺ�����ϵΪ![]()

��2����![]() ʱ�̵Ĵ�����Ϊ
ʱ�̵Ĵ�����Ϊ![]() �����������
�����������![]() ��
��
��
��![]() ʱ���䷽��������
ʱ���䷽��������![]()
����![]() ʱ��
ʱ��![]() ȡ������
ȡ������![]() �ϵ����ֵ100��
�ϵ����ֵ100��
��![]() ʱ���䷽��������
ʱ���䷽��������![]()
����![]() ʱ��
ʱ��![]() ȡ������
ȡ������![]() �ϵ����ֵ87��5��
�ϵ����ֵ87��5��
���Ͽ�֪![]() ������
������![]() �Ͽ���ȡ�����ֵ100����ʱ��
�Ͽ���ȡ�����ֵ100����ʱ��![]() �����Ӷ���һ�տ�ʼ�ĵ�50��ʱ�����е��������������100��
�����Ӷ���һ�տ�ʼ�ĵ�50��ʱ�����е��������������100��