题目内容
【题目】已知等差数列{an}的公差d≠0，它的前n项和为Sn，若S5＝70，且a2，a7，a22成等比数列．
(1)求数列{an}的通项公式；
(2)设数列
的前n项和为Tn，求证： 
≤Tn＜
.
【答案】（1）an＝4n＋2.（2）见解析
【解析】试题分析：
(1)由题意得到关于首项、公差的方程组，求解方程组可得a1＝6，d＝4.所以数列{an}的通项公式为an＝4n＋2(n∈N*)．
(2)裂项求和可得
，则
，结合前n项和公式可证得数列{Tn}是递增数列，则Tn≥T1＝
，据此即可证得题中的结论.
试题解析：
(1)因为数列{an}是等差数列，
所以an＝a1＋(n－1)d，Sn＝na1＋
d.
依题意，有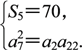
即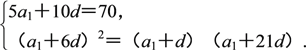
解得a1＝6，d＝4.
所以数列{an}的通项公式为an＝4n＋2(n∈N*)．
(2)证明：由(1)可得Sn＝2n2＋4n.
所以
＝
＝
＝
(
－
)．
所以Tn＝
＋
＋
＋…＋
＋＝
＋
＋
＋…＋·
＋
＝
＝
－
.
因为Tn－＝－＜0，所以Tn＜.
因为Tn＋1－Tn＝
＞0，所以数列{Tn}是递增数列，
所以Tn≥T1＝
.所以≤Tn＜.
练习册系列答案
教材全解字词句篇系列答案
相关题目
