题目内容

16．已知双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的左右焦点分别为F1、F2，若双曲线上一点P满足|PF1|•|PF2|=55，求点P到焦点的距离．

分析 利用双曲线的定义，结合|PF1|•|PF2|=55，求点P到焦点的距离．

解答 解：∵双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1，
∴a=3，
设|PF1|＞|PF2|，
则|PF1|-|PF2|=6，
∵|PF1|•|PF2|=55，
∴|PF1|=11，|PF2|=5．

点评 本题考查点P到焦点的距离的求法，解题时要熟练掌握双曲线的定义，比较基础．

练习册系列答案
相关题目
6．已知抛物线y2=4x，点P是抛物线上一动点，点M（4，2）是平面上的一定点，则|PM|+|PF|的最小值为5．
7．已知数列{an}的前n项和为Sn，且Sn=2n+1-2，n∈N*．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设数{an}满足bn=$\frac{{S}_{n}}{{a}_{n}}$，求数列{bn}的前n项和Tn．
4．一个几何体的三视图如图所示，则该几何体的体积为（　　）
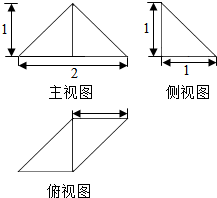
A．$\frac{1}{2}$B．1C．$\frac{1}{3}$D．$\frac{1}{6}$
11．已知F，A分别为双曲线 $\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点，右顶点，过F作x轴的垂线，在第一象限与双曲线交于点P，AP的延长线与双曲线的渐近线在第一象限交与点Q，若向量$\overrightarrow{AP}$=（2-$\sqrt{2}$）向量$\overrightarrow{AQ}$，则双曲线的离心率是$\sqrt{2}$．
1．设集合A={x|x≥3}，B={x|x≤3}，则A∩B=（　　）
A．∅B．RC．{x||x≤3}D．{3}
8．已知二次函数f（x）满足f（0）=1，单调减区间是（-∞，1]，最小值为-1，
（I）求函数f（x）的解析式；
（2）若x∈[0，3），求函数f（x）的值域．
5．若A={3，1，0}，B={1，0，x}，若A=B，则x=3．
17．已知角θ∈（0，2π），关于x的方程2x2-（$\sqrt{3}$-1）x+m=0的两根为sinθ，cosθ．
（1）求m的值；
（2）求方程的两根及此时θ的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网