题目内容
已知命题p:方程 2x2+ax-a2=0在[-1,1]上有解;命题q:只有一个实数x0满
2x2+ax-a2=0在[-1,1]上有解;命题q:只有一个实数x0满
足不等式x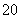 +2ax0+2a≤0,若命题“p或q”是假命题,
+2ax0+2a≤0,若命题“p或q”是假命题, 求a的取值范围.
求a的取值范围.
解 由2x2 +ax-a2=0得(2x-a)(x+a)=0, ∴x=
+ax-a2=0得(2x-a)(x+a)=0, ∴x=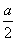 或x=-a,
或x=-a,
∴当命题p为真命题时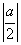 ≤1或|-a|≤1,∴|a|≤2.
≤1或|-a|≤1,∴|a|≤2.
又“只有一个实数x0满足x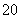 +2ax0+2a≤0”,
+2ax0+2a≤0”,
即抛物线y=x2+2ax+2a与x轴只有一个交点,
∴Δ=4a2-8a=0,∴a=0或a=2.
∴当命题q为真命题时,a=0或a=2.
∴命题“p或q”为真命题时,|a|≤2.
∵命题“p或q”为假命题,∴a>2或a<-2.
即a的取值范围为{a|a>2或a<-2}.

练习册系列答案
相关题目
某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产.已
知投资生产这两种产品的有关数据如下表:(单位:万美元)
| 项目类别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 |
| A产品 | 20 | m | 10 | 200 |
| B产品 | 40 | 8 | 18 | 120 |
其中年固定成本与年生产的件数无关,m为待定 常数,其值由生产A产品的原材料价格决定,预计m∈[6,8].另外,年销售x件B产品时需上
常数,其值由生产A产品的原材料价格决定,预计m∈[6,8].另外,年销售x件B产品时需上 交0.05x2万美元的特别关税.假设生产出来的产品都能在当年销售出去.
交0.05x2万美元的特别关税.假设生产出来的产品都能在当年销售出去.
(1)写出该厂分别投资生产A、B两种产品的年利润y1,y2与生产相应产品的件数x之间的函数关系并指明其定义域;
(2)如何投资才可获得最大年利润?请你做出规划.
 ,0)时,f(x)=2ax+
,0)时,f(x)=2ax+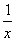 (a为实数).
(a为实数). }
} ,B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
,B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.