题目内容
设数列![]() 的前
的前![]() 项
项![]() 和为
和为![]() .已知
.已知![]()
![]() ,
,![]() ,
,![]() .
.
(Ⅰ)设![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]()
![]() ,证明对任意的
,证明对任意的![]() ,不等式
,不等式
![]() 恒成立.
恒成立.
![]()
解析:
(Ⅰ)解:依题意,![]() ,即
,即![]() ,
,
由此得![]() .
.
因此,所求通项公式为![]() ,
,![]() .……………………5分
.……………………5分
(Ⅱ)证明:由已知![]() ,
,
则![]() ,所以
,所以
![]() .……………………7分
.……………………7分
下面用数学归纳法证明不等式
![]() 成立.
成立.
①当![]() 时,左边=
时,左边=![]() ,右边=
,右边=![]() ,因为
,因为![]() ,所以不等式成立. …………………8分
,所以不等式成立. …………………8分
②假设当![]() 时不等式成立
时不等式成立![]() ,即
,即
![]() 成立.
成立.
则当![]() 时,左边
时,左边
=![]()
![]()
![]()
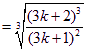 .……………………………………………………………………………11分
.……………………………………………………………………………11分
要证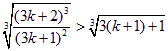 成立,
成立,
只需证![]() 成立,
成立,
由于![]() ,
,
只需证![]() 成立,
成立,
只需证![]() 成立,
成立,
只需证![]()
![]() 成立,
成立,
由于![]() ,所以
,所以![]() 成立.
成立.
即![]()
![]() 成立.
成立.
所以当![]()
![]() 时,不等式也成立.
时,不等式也成立.
由①,②可得不等式恒成立. ………………………………………………………………14分

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,已知
,已知 .
. ;
; 的前
的前 项和为
项和为 。已知
。已知 ,
, ,
, 。
。 ,求数列
,求数列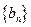 的通项公式;
的通项公式; ,
, 的取值范围。
的取值范围。 的前
的前 项和为
项和为 ,已知
,已知
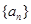 为等差数列,并写出
为等差数列,并写出 关于
关于 前
前 ,问满足
,问满足 的最小正整数
的最小正整数