题目内容
设数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,且
,且
![]() ,
,
其中![]() 为常数.
为常数.
(Ⅰ)求![]() 与
与![]() 的值;
的值;
(Ⅱ)证明:数列![]() 为等差数列;
为等差数列;
(Ⅲ)证明:不等式![]() 对任何正整数
对任何正整数![]() 都成立.
都成立.
![]() ,
,![]() .
.
解析:
解:(Ⅰ)由已知,得![]() ,
,![]() ,
,![]() .
.
由![]() ,知
,知
![]() 即
即 ![]()
解得 ![]() ,
,![]() .
.
(Ⅱ)方法1
由(Ⅰ),得 ![]() , ①
, ①
所以 ![]() . ②
. ②
②-①,得 ![]() , ③
, ③
所以 ![]() . ④
. ④
④-③,得 ![]() .
.
因为 ![]() ,
,
所以 ![]() .
.
又因为 ![]() ,
,
所以 ![]() ,
,
即 ![]() ,
,![]() .
.
所以数列![]() 为等差数列.
为等差数列.
方法2
由已知,得![]() ,
,
又![]() ,且
,且![]() ,
,
所以数列![]() 是唯一确定的,因而数列
是唯一确定的,因而数列![]() 是唯一确定的.
是唯一确定的.
设![]() ,则数列
,则数列![]() 为等差数列,前
为等差数列,前![]() 项和
项和![]() .
.
于是 ![]() ,
,
由唯一性得 ![]() ,即数列
,即数列![]() 为等差数列.
为等差数列.
(Ⅲ)由(Ⅱ)可知,![]() .
.
要证 ![]() ,
,
只要证 ![]() .
.
因为 ![]() ,
,![]() ,
,
故只要证 ![]() ,
,
即只要证 ![]() .
.
因为 ![]()
![]()
![]() ,
,
所以命题得证.

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,已知
,已知 .
. ;
; 的前
的前 项和为
项和为 。已知
。已知 ,
, ,
, 。
。 ,求数列
,求数列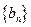 的通项公式;
的通项公式; ,
, 的取值范围。
的取值范围。 的前
的前 项和为
项和为 ,已知
,已知
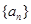 为等差数列,并写出
为等差数列,并写出 关于
关于 前
前 ,问满足
,问满足 的最小正整数
的最小正整数