题目内容
已知函数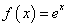
．
（I）当
时，设
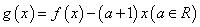．讨论函数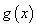
的单调性；
（II）证明当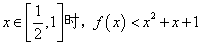
．
解：（Ⅰ）
，所以
．……………………2分
当
时，
，故有：当
，即
时，
，
；
当
，即
时，，
令，得
；令
，得
，………………………5分
综上，当时，
在
上是增函数；
当时，在
上是减函数，在
上是增函数．………6分
（Ⅱ）设
，则
，
令
，则
， …………………………………8分
因为
，所以当
时，
；
在
上是减函数，
当
时，
，在
上是增函数，
又
所以当时,恒有
,即
,所以
在
上为减函数，所以
，
即当时，
． …………………………………………13分
练习册系列答案
相关题目
为圆O的直径，C、D是圆O上的两个点，
于
，
交
于
，
于
，
． 
：
上的任意两点，且
，若线段PQ的中点组成的区域为M，在圆O内任取一点，则该点落在区域M内的概率为 （ ）
B．
C．
D．
，则函数
的零点个数为___________．
