题目内容
下列结论中,正确的是( )
①命题“如果 ,则
,则 ”的逆否命题是“如果
”的逆否命题是“如果 ,则
,则 ”;
”;
②已知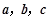 为非零的平面向量.甲:
为非零的平面向量.甲: ,乙:
,乙: ,则甲是乙的必要条件,但不是充分条件;
,则甲是乙的必要条件,但不是充分条件;
③ 是周期函数,
是周期函数, 是周期函数,则
是周期函数,则 是真命题;
是真命题;
④命题 的否定是:
的否定是: .
.
| A.①② | B.①④ | C.①②④ | D.①③④ |
C
解析试题分析:由原命题和逆否命题的关系知①正确;由 可得
可得 或
或 与向量
与向量 垂直,所以②正确;③中命题
垂直,所以②正确;③中命题 是假命题,所以
是假命题,所以 是假命题,所以③错误;特称命题的否定是全称命题,所以④正确.
是假命题,所以③错误;特称命题的否定是全称命题,所以④正确.
考点:本小题主要考查原命题与逆否命题的关系、充要条件的判断、含逻辑联结词的命题的真假和特称命题的否定,考查学生对概念性问题的理解和应用.
点评:由 得不出
得不出 ,这是学生容易忽略的问题,一定要特别注意.
,这是学生容易忽略的问题,一定要特别注意.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
“ ”是“
”是“ ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
“ ”是“对任意的正数
”是“对任意的正数 ,
, 恒成立”的( )
恒成立”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知 ,那么“
,那么“ ”是 “
”是 “ ”的( )
”的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
设 ,
, 是定义在R上的函数,
是定义在R上的函数, ,则“
,则“ ,
, 均为偶函数”是“
均为偶函数”是“ 为偶函数”的( )
为偶函数”的( )
| A.充分而不必要的条件 | B.必要而不充分的条件 |
| C.充分必要条件 | D.既不充分也不必要的条件 |
设 ,则“
,则“ ”是“直线
”是“直线 与直线
与直线 平行的( )
平行的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列命题是真命题的是
①“若 ,则
,则 不全为零”的否命题;
不全为零”的否命题;
②“正六边形都相似”的逆命题;
③“若 ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;
④“若 是有理数,则
是有理数,则 是无理数”.
是无理数”.
| A.①④ | B.③④ | C.①③④ | D.①②③④ |
下列命题的否定是真命题的有① ②
② 所有的正方形都是矩形③
所有的正方形都是矩形③ ④
④ 至少有一个实数
至少有一个实数 使
使 ( )
( )
| A.1个 | B.2个 | C.3个 | D.4个 |
 ,则“
,则“ ”是 “
”是 “ ”的( )
”的( )