题目内容
设 ,
, 是定义在R上的函数,
是定义在R上的函数, ,则“
,则“ ,
, 均为偶函数”是“
均为偶函数”是“ 为偶函数”的( )
为偶函数”的( )
| A.充分而不必要的条件 | B.必要而不充分的条件 |
| C.充分必要条件 | D.既不充分也不必要的条件 |
A
解析试题分析:因为函数f(x),g(x)都是偶函数,那么根据偶函数的定义可知f(-x)="f(x)," g(-x)=g(x),那么f(x)+g(x)=f(-x)+g(-x),可知h(x)=h(-x),说明函数h(x)是偶函数,那么如果函数h(x)为偶函数,即h(x)=h(-x),故有f(x)+g(x)=f(-x)+g(-x),但是不一定得到f(-x)="f(x)," g(-x)=g(x),故不成立,因此得到条件是结论成立的充分不必要条件,选A.
考点:本试题主要考查了函数的奇偶性和充分条件的判定的运用。
点评:解决该试题的关键是偶函数的定义的理解和运用。

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
设p、q是两上命题, ( )
( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“存在一个无理数,它的平方是有理数”的否定是( )
| A.任意一个无理数,它的平方是有理数 |
| B.任意一个无理数,它的平方不是有理数 |
| C.存在一个有理数,它的平方是有理数 |
| D.存在一个有理数,它的平方不是有理数 |
命题“对任意的 ”的否定是( )
”的否定是( )
A.不存在 | B.存在 |
C.存在 | D.对任意的 |
已知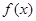 是定义在R上的偶函数,且以2为周期,则“
是定义在R上的偶函数,且以2为周期,则“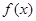 为[0,1]上的增函数”是“
为[0,1]上的增函数”是“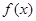 为[3,4]上的减函数”的( )
为[3,4]上的减函数”的( )
| A.既不充分也不必要的条件 | B.充分而不必要的条件 |
| C.必要而不充分的条件 | D.充要条件 |
下列结论中,正确的是( )
①命题“如果 ,则
,则 ”的逆否命题是“如果
”的逆否命题是“如果 ,则
,则 ”;
”;
②已知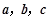 为非零的平面向量.甲:
为非零的平面向量.甲: ,乙:
,乙: ,则甲是乙的必要条件,但不是充分条件;
,则甲是乙的必要条件,但不是充分条件;
③ 是周期函数,
是周期函数, 是周期函数,则
是周期函数,则 是真命题;
是真命题;
④命题 的否定是:
的否定是: .
.
| A.①② | B.①④ | C.①②④ | D.①③④ |
有下列四个命题:①“若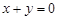 ,则
,则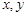 互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“若
互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“若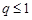 ,则
,则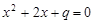 有实根”的逆命题;④“不等边三角形的三个内角相等”的逆否命题;其中真命题有( )
有实根”的逆命题;④“不等边三角形的三个内角相等”的逆否命题;其中真命题有( )
| A.①② | B.②③ | C.①③ | D.③④ |
已知命题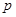 :
: ,则( )
,则( )
A.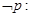 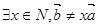 | B.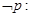  |
C.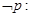 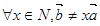 | D.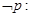  |
 >0”的充分不必要条件
>0”的充分不必要条件