题目内容
12．已知m，n∈R，集合A={2，log2m}，集合B={m，n}，若A∩B={1，2}，则m+n=（ ）| A． | 1 | B． | 2 | C． | 4 | D． | 3 |
分析 由交集性质得1∈A，1∈B，从而能出m=2，n=1，进而能求出m+n的值．
解答 解：∵m，n∈R，集合A={2，log2m}，集合B={m，n}，若A∩B={1，2}，
∴1∈A，1∈B，
∴$\left\{\begin{array}{l}{lo{g}_{2}m=1}\\{n=1}\end{array}\right.$，解得m=2，n=1，
∴m+n=3．
故选：D．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．
练习册系列答案
相关题目
2．数列{an}中，${a_1}+{a_2}+{a_3}+…+{a_n}={3^n}-1$，则${a_1}^2+{a_2}^2+{a_3}^2+…+{a_n}^2$等于（ ）
| A． | 9n-1 | B． | （3n-1）2 | C． | $\frac{1}{2}（{{9^n}-1}）$ | D． | $\frac{3}{4}（{{3^n}-1}）$ |
17．已知a1，x，y，a2成等差数列，b1，x，y，b2成等比数列．则$\frac{{{{（{{a_1}+{a_2}}）}^2}}}{{{b_1}{b_2}}}-2$的取值范围是（ ）
| A． | （0，2] | B． | [-2，0）∪（0，2] | C． | （-∞，-2]∪[2，+∞） | D． | （-∞，-1]∪[1，+∞） |
4．在区间[0，9]上随机取一实数x，则该实数x满足不等式1≤log2x≤2的概率为（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{2}{9}$ | C． | $\frac{4}{9}$ | D． | $\frac{7}{9}$ |
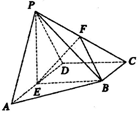在四棱锥P-ABCD中，E为棱AD的中点，PE⊥平面ABCD，AD∥BC，∠ADC=90°，ED=BC=2，EB=3，F为棱PC的中点．