题目内容
已知函数f(x)＝2ax－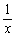
－(2＋a)lnx(a≥0).
（1）当a＝0时，求f(x)的极值；
（2）当a＞0时，讨论f(x)的单调性；
（3）若对任意的a∈(2, 3)，x1, x2∈[1, 3]，恒有(m－ln3)a－2ln3＞|f(x1)－f(x2)|成立，求实数m的取值范围。
解：（1）当
时，
由
,解得
，可知
在
上是增函数，在
上是减函数.
∴的极大值为
，无极小值.
.①当
时，在和
上是增函数，在
上是减函数；
②当
时，在
上是增函数；
③当
时，在
和上是增函数，在
上是减函数
（3）当
时，由（2）可知在
上是增函数，
∴
.
由
对任意的a∈(2, 3)，x1, x2∈[1, 3]恒成立，
∴
即
对任意恒成立，
即
对任意恒成立， …
由于当时，
，∴
.
练习册系列答案
相关题目
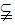β，给出下列四个命题：
内投点，点落在区域的每个位置是等可能的，则坐标原点与该点连线的倾斜角小于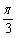
的概率为 。
与圆x2＋y2＝a2＋b2的一个交点，F1, F2分别是双曲线的左、右焦点，且|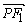
|＝
|
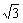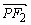|，则双曲线的离心率为
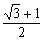B．
＝
.
，则实数
等于 （ ） A．
B．1 C．
D．
=
上是减函数，则
的取值范围是 。 
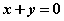, 则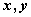
互为相反数”的逆命题； 
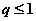,则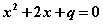
有实根”的逆否命题；
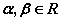，使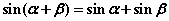
成立”的否定．
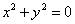，则x,y全为0”的逆命题；
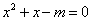有实根”的逆否命题；
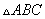中，
、
、
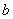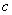分别是角A、B、C所对的边长，若
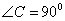,则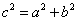
”的逆否命题。