题目内容
已知实数m为非零常数,且f(x)=loga(1+
)(a>0且a≠1)为奇函数.
(1)求m的值;
(2)判断f(x)在区间(1,+∞)上的单调性,并用单调性定义加以证明;
(3)当x∈(b,a)时,函数f(x)的值域为(1,+∞),请确定实数a与b的取值.
| m |
| x-1 |
(1)求m的值;
(2)判断f(x)在区间(1,+∞)上的单调性,并用单调性定义加以证明;
(3)当x∈(b,a)时,函数f(x)的值域为(1,+∞),请确定实数a与b的取值.
(1)若函数f(x)=loga(1+
)(a>0且a≠1)为奇函数
故f(-x)+f(x)=loga(1+
)+loga(1+
)=loga[(1+
)(1+
)]=loga[
]=0
即
=1,即(m-1)2=1
∵m≠0,
∴m=2
(2)由(1)得f(x)=loga(1+
)=loga(
),
当0<a<1时,函数在区间(1,+∞)上为增函数
当a>1时,函数在区间(1,+∞)上为减函数,理由如下:
令x1,x2是区间(1,+∞)上的任意两个值,且x1<x2,
则x2-x1>0,x1-1>0,x2+1>0,1+
>1
则f(x1)-f(x2)=loga(
)-loga(
)=loga(
•
)=loga[1+
]
当0<a<1时,f(x1)-f(x2)<0,即f(x1)<f(x2),函数在区间(1,+∞)上为增函数
当a>1时,f(x1)-f(x2)>0,即f(x1)>f(x2),函数在区间(1,+∞)上为减函数
(3)由(1)得f(x)=loga(
)的定义域为(-∞,-1)∪(1,+∞),
当0<a<1时,(b,a)?(-∞,-1)∪(1,+∞),此时函数的解析式无意义;
当a>1,若函数的解析式有意义,则1≤b<a,
由(2)可得,此时函数在(b,a)上为减函数
若函数f(x)的值域为(1,+∞)
则f(a)=1,
即loga(
)=1
即
=a
解得a=1+
且
(1+
)=+∞
解得b=1
综上,a=1+
,b=1
| m |
| x-1 |
故f(-x)+f(x)=loga(1+
| m |
| -x-1 |
| m |
| x-1 |
| m |
| x-1 |
| m |
| -x-1 |
| -x2+(m-1)2 |
| 1-x2 |
即
| -x2+(m-1)2 |
| 1-x2 |
∵m≠0,
∴m=2
(2)由(1)得f(x)=loga(1+
| 2 |
| x-1 |
| x+1 |
| x-1 |
当0<a<1时,函数在区间(1,+∞)上为增函数
当a>1时,函数在区间(1,+∞)上为减函数,理由如下:
令x1,x2是区间(1,+∞)上的任意两个值,且x1<x2,
则x2-x1>0,x1-1>0,x2+1>0,1+
| 2(x2-x1) |
| (x1-1)•(x2+1) |
则f(x1)-f(x2)=loga(
| x1+1 |
| x1-1 |
| x2+1 |
| x2-1 |
| x1+1 |
| x1-1 |
| x2-1 |
| x2+1 |
| 2(x2-x1) |
| (x1-1)•(x2+1) |
当0<a<1时,f(x1)-f(x2)<0,即f(x1)<f(x2),函数在区间(1,+∞)上为增函数
当a>1时,f(x1)-f(x2)>0,即f(x1)>f(x2),函数在区间(1,+∞)上为减函数
(3)由(1)得f(x)=loga(
| x+1 |
| x-1 |
当0<a<1时,(b,a)?(-∞,-1)∪(1,+∞),此时函数的解析式无意义;
当a>1,若函数的解析式有意义,则1≤b<a,
由(2)可得,此时函数在(b,a)上为减函数
若函数f(x)的值域为(1,+∞)
则f(a)=1,
即loga(
| a+1 |
| a-1 |
即
| a+1 |
| a-1 |
解得a=1+
| 2 |
且
| lim |
| x→b |
| 2 |
| x-1 |
解得b=1
综上,a=1+
| 2 |

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
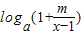 (a>0且a≠1)为奇函数.
(a>0且a≠1)为奇函数.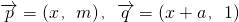 ,二次函数
,二次函数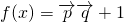 ,关于x的不等式f(x)>(2m-1)x+1-m2的解集为(-∞,m)∪(m+1,+∞),其中m为非零常数,设
,关于x的不等式f(x)>(2m-1)x+1-m2的解集为(-∞,m)∪(m+1,+∞),其中m为非零常数,设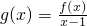 .
.