题目内容
已知实数m为非零常数,且f(x)=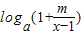 (a>0且a≠1)为奇函数.
(a>0且a≠1)为奇函数.(1)求m的值;
(2)判断f(x)在区间(1,+∞)上的单调性,并用单调性定义加以证明;
(3)当x∈(b,a)时,函数f(x)的值域为(1,+∞),请确定实数a与b的取值.
【答案】分析:(1)由函数f(x)= (a>0且a≠1)为奇函数,根据奇函数的定义可得f(-x)+f(x)=0,进而求出非零m的值;
(a>0且a≠1)为奇函数,根据奇函数的定义可得f(-x)+f(x)=0,进而求出非零m的值;
(2)x1,x2是区间(1,+∞)上的任意两个值,且x1<x2,可得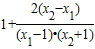 >1,分当0<a<1时和当a>1时两种情况,结合复合函数的单调性,可证明函数的单调性;
>1,分当0<a<1时和当a>1时两种情况,结合复合函数的单调性,可证明函数的单调性;
(3)由函数解析式求出函数的定义域,结合(2)中函数的单调性,进而根据当x∈(b,a)时,函数f(x)的值域为(1,+∞),可得f(a)=1且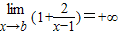 ,解方程可求出a,b的值.
,解方程可求出a,b的值.
解答:解:(1)若函数f(x)=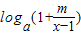 (a>0且a≠1)为奇函数
(a>0且a≠1)为奇函数
故f(-x)+f(x)=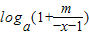 +
+ =
=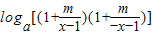 =
=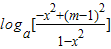 =0
=0
即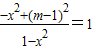 ,即(m-1)2=1
,即(m-1)2=1
∵m≠0,
∴m=2
(2)由(1)得f(x)=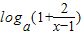 =
=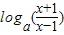 ,
,
当0<a<1时,函数在区间(1,+∞)上为增函数
当a>1时,函数在区间(1,+∞)上为减函数,理由如下:
令x1,x2是区间(1,+∞)上的任意两个值,且x1<x2,
则x2-x1>0,x1-1>0,x2+1>0,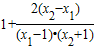 >1
>1
则f(x1)-f(x2)=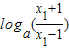 -
-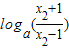 =
=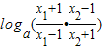 =
=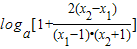
当0<a<1时,f(x1)-f(x2)<0,即f(x1)<f(x2),函数在区间(1,+∞)上为增函数
当a>1时,f(x1)-f(x2)>0,即f(x1)>f(x2),函数在区间(1,+∞)上为减函数
(3)由(1)得f(x)=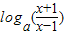 的定义域为(-∞,-1)∪(1,+∞),
的定义域为(-∞,-1)∪(1,+∞),
当0<a<1时,(b,a)?(-∞,-1)∪(1,+∞),此时函数的解析式无意义;
当a>1,若函数的解析式有意义,则1≤b<a,
由(2)可得,此时函数在(b,a)上为减函数
若函数f(x)的值域为(1,+∞)
则f(a)=1,
即 =1
=1
即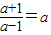
解得a=1+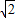
且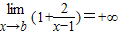
解得b=1
综上,a=1+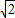 ,b=1
,b=1
点评:本题考查的知识点是函数的奇偶性,函数的单调性,函数的值域,熟练掌握函数奇偶性和函数单调性的定义是解答的关键.
 (a>0且a≠1)为奇函数,根据奇函数的定义可得f(-x)+f(x)=0,进而求出非零m的值;
(a>0且a≠1)为奇函数,根据奇函数的定义可得f(-x)+f(x)=0,进而求出非零m的值;(2)x1,x2是区间(1,+∞)上的任意两个值,且x1<x2,可得
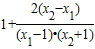 >1,分当0<a<1时和当a>1时两种情况,结合复合函数的单调性,可证明函数的单调性;
>1,分当0<a<1时和当a>1时两种情况,结合复合函数的单调性,可证明函数的单调性;(3)由函数解析式求出函数的定义域,结合(2)中函数的单调性,进而根据当x∈(b,a)时,函数f(x)的值域为(1,+∞),可得f(a)=1且
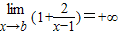 ,解方程可求出a,b的值.
,解方程可求出a,b的值.解答:解:(1)若函数f(x)=
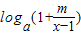 (a>0且a≠1)为奇函数
(a>0且a≠1)为奇函数故f(-x)+f(x)=
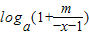 +
+ =
=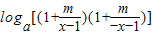 =
=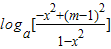 =0
=0即
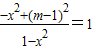 ,即(m-1)2=1
,即(m-1)2=1∵m≠0,
∴m=2
(2)由(1)得f(x)=
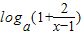 =
=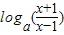 ,
,当0<a<1时,函数在区间(1,+∞)上为增函数
当a>1时,函数在区间(1,+∞)上为减函数,理由如下:
令x1,x2是区间(1,+∞)上的任意两个值,且x1<x2,
则x2-x1>0,x1-1>0,x2+1>0,
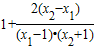 >1
>1则f(x1)-f(x2)=
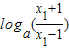 -
-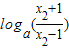 =
=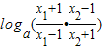 =
=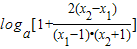
当0<a<1时,f(x1)-f(x2)<0,即f(x1)<f(x2),函数在区间(1,+∞)上为增函数
当a>1时,f(x1)-f(x2)>0,即f(x1)>f(x2),函数在区间(1,+∞)上为减函数
(3)由(1)得f(x)=
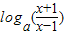 的定义域为(-∞,-1)∪(1,+∞),
的定义域为(-∞,-1)∪(1,+∞),当0<a<1时,(b,a)?(-∞,-1)∪(1,+∞),此时函数的解析式无意义;
当a>1,若函数的解析式有意义,则1≤b<a,
由(2)可得,此时函数在(b,a)上为减函数
若函数f(x)的值域为(1,+∞)
则f(a)=1,
即
 =1
=1即
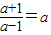
解得a=1+
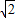
且
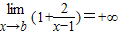
解得b=1
综上,a=1+
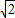 ,b=1
,b=1点评:本题考查的知识点是函数的奇偶性,函数的单调性,函数的值域,熟练掌握函数奇偶性和函数单调性的定义是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
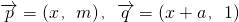 ,二次函数
,二次函数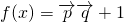 ,关于x的不等式f(x)>(2m-1)x+1-m2的解集为(-∞,m)∪(m+1,+∞),其中m为非零常数,设
,关于x的不等式f(x)>(2m-1)x+1-m2的解集为(-∞,m)∪(m+1,+∞),其中m为非零常数,设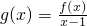 .
.