题目内容
点P是![]() 为焦点的双曲线
为焦点的双曲线![]() 上的一点,已知
上的一点,已知![]() ,
,![]() ,O为坐标原点。
,O为坐标原点。
(1)求双曲线的离心率![]() ;
;
(2)过点P作直线分别与双曲线两渐近线相交于![]() 两点,且
两点,且![]() ,
,![]() 求双曲线E的方程;
求双曲线E的方程;
(3)若过点Q(m,0)(m为非零常数)的直线![]() 与(2)中的双曲线E相交于不同于双曲线顶点的两点M、N,且
与(2)中的双曲线E相交于不同于双曲线顶点的两点M、N,且![]() (
(![]() 为非零实数),问在
为非零实数),问在![]() 轴上是否存在定点G使
轴上是否存在定点G使![]() ?若存在,求出所有这种定点G的坐标;若不存在,请说明理由。
?若存在,求出所有这种定点G的坐标;若不存在,请说明理由。
解:(1)∵![]() ,
,![]() ,
,
∴![]() ,
,![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]() 。
。
(2)由(1)知双曲线的方程可设为![]() ,渐近线方程
,渐近线方程![]()
设![]()
∵![]() ,
,
∵
∵点P在双曲线上,
∴![]()
化简得![]() ,∴
,∴![]() ,∴
,∴![]()
∴双曲线方程为![]() 。
。
(3)设在![]() 轴上存在定点G(t,0),使
轴上存在定点G(t,0),使![]()
①若直线![]()
![]() 轴,
轴,![]() (确保直线
(确保直线![]() 与双曲线E有两个不同交点)
与双曲线E有两个不同交点)
![]() 时,则有
时,则有![]() ,且对
,且对![]() 轴上任一点G,
轴上任一点G,
![]() ,
,![]()
②若直线![]() 不垂直
不垂直![]() 轴,设直线
轴,设直线![]() :
:![]() ,
,![]() ,
,![]()
联立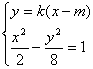 得
得![]()
![]() ,
,![]()
∵![]() ,
,
![]()
![]() 的充要条件为
的充要条件为![]()
由![]() 得
得![]() ,∴
,∴![]() ,
,
又∵![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
综上,在![]() 轴上存在一点
轴上存在一点![]() ,使得
,使得![]() 。
。

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
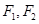 为焦点的双曲线
为焦点的双曲线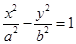 上一点,满足
上一点,满足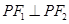 ,且
,且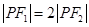 ,则此双曲线的离心率为 .
,则此双曲线的离心率为 . 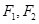 为焦点的双曲线
为焦点的双曲线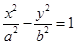 上一点,满足
上一点,满足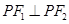 ,且
,且 ,
,