题目内容
已知A是曲线ρ=3cosθ上任意一点,求点A到直线ρ=| 1 | 4cosθ+3sinθ |
分析:先把极坐标转化为直角坐标方程,利用圆心到直线的距离加上半径可求最大值.
解答:解:将极坐标方程转化成直角坐标方程:ρ=3cosθ,得x2+y2=3x,即(x-
)2+y2=
,
ρ=
即:4x+3y-1=0;
圆心到直线的距离为:d=
=1
所以点A到直线距离的最大值为1+
=
.
| 3 |
| 2 |
| 9 |
| 4 |
ρ=
| 1 |
| 4cosθ+3sinθ |
圆心到直线的距离为:d=
|4×
| ||
| 5 |
所以点A到直线距离的最大值为1+
| 3 |
| 2 |
| 5 |
| 2 |
点评:本题考查点的极坐标和直角坐标的互化,点到直线的距离公式,考查分析问题解决问题的能力,是中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
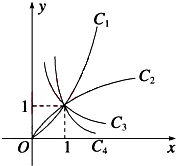 图中曲线是幂函数y=xn在第一象限的图象,已知n取±3,±
图中曲线是幂函数y=xn在第一象限的图象,已知n取±3,±| 1 |
| 3 |
A、-3,-
| ||||
B、3,
| ||||
C、-
| ||||
D、3,
|