题目内容
将奇函数f(x)=Asin(ωx+?)(A≠0,ω>0,-
<?<
)的图象向左平移
个单位得到的图象关于原点对称,则ω的值最小值为
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
6
6
.分析:求出奇函数函数平移后的函数的解析式,利用函数图象关于原点对称,计算函数的是奇函数,求出ω的值最小值.
解答:解:奇函数f(x)=Asin(ωx+?)(A≠0,ω>0,-
<?<
),所以?=0,
函数的图象向左平移
个单位得到函数f(x)=Asin(ωx+
),它的函数图象关于原点对称,所以
=kπ,k∈Z,所以ω的值最小值为6.
故答案为:6.
| π |
| 2 |
| π |
| 2 |
函数的图象向左平移
| π |
| 6 |
| ωπ |
| 6 |
| ωπ |
| 6 |
故答案为:6.
点评:本题考查函数的平移,函数的奇偶性,注意三角函数的诱导公式的应用,考查计算能力.

练习册系列答案
相关题目
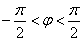 )的图象向左平移
)的图象向左平移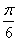 个单位得到的图象关于原点对称,则ω的值可以为
个单位得到的图象关于原点对称,则ω的值可以为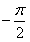 <ψ<
<ψ<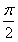 )的图象向左平移
)的图象向左平移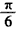 个单位得到的图象关于原点对称,则ω的值可以为
个单位得到的图象关于原点对称,则ω的值可以为