题目内容
13.已知圆心为C的圆过原点O(0,0),且直线2x-y+2=0与圆C相切于点P(0,2).(1)求圆C的方程;
(2)已知过点Q(0,1)的直线l的斜率为k,且直线l与圆C相交于A,B两点.
①若k=2,求弦AB的长;
②若圆C上存在点D,使得$\overrightarrow{CA}$+$\overrightarrow{CB}$=$\overrightarrow{CD}$,求直线l的斜率k.
分析 (1)设圆的方程为x2+y2+Dx+Ey=0,4+2E=0,∴$\frac{2-1}{\frac{D}{2}}=-\frac{1}{2}$,解得D、E即可;
(2)①直线l的方程为:y=2x+1,由圆心到直线l的距离为d=$\frac{2×2-1+1}{\sqrt{5}}=\frac{4}{\sqrt{5}}$,可得$AB=2\sqrt{{R}^{2}-{d}^{2}}$=$\frac{6\sqrt{5}}{5}$.
②由$\overrightarrow{CA}$+$\overrightarrow{CB}$=$\overrightarrow{CD}$,得四边形CADB为菱形,即C到直线AB的距离为半径的一半,设直线l的方程为:y=kx+1,$\frac{|2k-1+1|}{\sqrt{{k}^{2}+1}}=\frac{\sqrt{5}}{2}$解得k.
解答 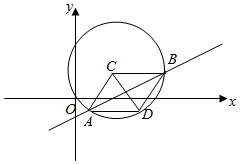 解:(1)设圆的方程为x2+y2+Dx+Ey=0,
解:(1)设圆的方程为x2+y2+Dx+Ey=0,
∵点(0,2)在圆上,∴4+2E=0,∴E=-2,
∵直线2x-y+2=0与圆C相切,∴$\frac{2-1}{\frac{D}{2}}=-\frac{1}{2}$,解得D=-4,
∴圆C的方程:x2+y2-4x-2y=0.
(2)①直线l的方程为:y=2x+1,即2x-y+1=0,
圆C的圆心为(2,1),半径为R=$\sqrt{5}$,
圆心到直线l的距离为d=$\frac{2×2-1+1}{\sqrt{5}}=\frac{4}{\sqrt{5}}$,
∴$AB=2\sqrt{{R}^{2}-{d}^{2}}$=$\frac{6\sqrt{5}}{5}$.
②如图,∵$\overrightarrow{CA}$+$\overrightarrow{CB}$=$\overrightarrow{CD}$,∴四边形CADB为菱形,
∴C到直线AB的距离为半径的一半,
设直线l的方程为:y=kx+1,
$\frac{|2k-1+1|}{\sqrt{{k}^{2}+1}}=\frac{\sqrt{5}}{2}$,
解得k=$±\frac{\sqrt{55}}{11}$,
∴直线l的斜率k为$±\frac{\sqrt{55}}{11}$.
点评 本题考查了圆的方程,直线与椭圆的位置关系,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\sqrt{6}$ | B. | 2$\sqrt{6}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲(x) | 89 | 91 | 93 | 95 | 97 |
| 乙(y) | 87 | 89 | 89 | 92 | 93 |
(2)根据表中数据,求乙分数y对甲分数x的回归方程;
( 附:回归方程y=bx+a中,a=$\overline{y}$-$\overline{bx}$,b=$\frac{\sum_{1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{1}^{n}({x}_{i}-\overline{x})^{2}}$)
| A. | 81 | B. | 64 | C. | 32 | D. | 27 |
| A. | 2 | B. | $\frac{1}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
| A. | 4x-y+3=0 | B. | 4x-y-3=0 | C. | 4x+y+3=0 | D. | 4x+y-3=0 |
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{8}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{8}$ |