题目内容
在棱长为3的正四面体ABCD中,点E是线段AB上一点,且AE=1,点F是线段AD上一点,且AF=2,则异面直线DE与CF的夹角的余弦为 .
【答案】分析:在AB上取一点M,使AM= ,由于
,由于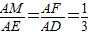 ,可得MF∥ED,则∠CFM或其补角,即为异面直线DE与CF的夹角.利用余弦定理求得CF2、MF2、CM2 的值,再在△CFM中,利用余弦定理求得cos∠CFM 得值,再取绝对值,即得所求.
,可得MF∥ED,则∠CFM或其补角,即为异面直线DE与CF的夹角.利用余弦定理求得CF2、MF2、CM2 的值,再在△CFM中,利用余弦定理求得cos∠CFM 得值,再取绝对值,即得所求.
解答: 解:∵在棱长为3的正四面体ABCD中,点E是线段AB上一点,且AE=1,点F是线段AD上一点,且AF=2,
解:∵在棱长为3的正四面体ABCD中,点E是线段AB上一点,且AE=1,点F是线段AD上一点,且AF=2,
在AB上取一点M,使AM= ,如图所示:
,如图所示:
由于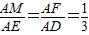 ,∴MF∥ED,则∠CFM或其补角,即为异面直线DE与CF的夹角.
,∴MF∥ED,则∠CFM或其补角,即为异面直线DE与CF的夹角.
△CDF中,由余弦定理可得 CF2=9+4-2×3×2cos60°=7,△CAM中,由余弦定理可得 CM2=9+ -2×3×
-2×3× ×cos60°=
×cos60°= ,
,
△AMF中,由余弦定理可得 MF2= +1-2×
+1-2× ×1×cos60°=
×1×cos60°= .
.
在△CFM中,由余弦定理可得CM2=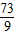 =7+
=7+ -2×
-2×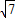 ×
×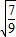 ×cos∠CFM,解得cos∠CFM=-
×cos∠CFM,解得cos∠CFM=-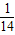 ,
,
故异面直线DE与CF的夹角的余弦为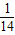 ,
,
故答案为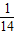 .
.
点评:本题主要考查异面直线所成的角的定义和求法,余弦定理的应用,体现了数形结合的数学思想,属于中档题.
 ,由于
,由于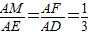 ,可得MF∥ED,则∠CFM或其补角,即为异面直线DE与CF的夹角.利用余弦定理求得CF2、MF2、CM2 的值,再在△CFM中,利用余弦定理求得cos∠CFM 得值,再取绝对值,即得所求.
,可得MF∥ED,则∠CFM或其补角,即为异面直线DE与CF的夹角.利用余弦定理求得CF2、MF2、CM2 的值,再在△CFM中,利用余弦定理求得cos∠CFM 得值,再取绝对值,即得所求.解答:
 解:∵在棱长为3的正四面体ABCD中,点E是线段AB上一点,且AE=1,点F是线段AD上一点,且AF=2,
解:∵在棱长为3的正四面体ABCD中,点E是线段AB上一点,且AE=1,点F是线段AD上一点,且AF=2,在AB上取一点M,使AM=
 ,如图所示:
,如图所示:由于
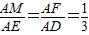 ,∴MF∥ED,则∠CFM或其补角,即为异面直线DE与CF的夹角.
,∴MF∥ED,则∠CFM或其补角,即为异面直线DE与CF的夹角.△CDF中,由余弦定理可得 CF2=9+4-2×3×2cos60°=7,△CAM中,由余弦定理可得 CM2=9+
 -2×3×
-2×3× ×cos60°=
×cos60°= ,
,△AMF中,由余弦定理可得 MF2=
 +1-2×
+1-2× ×1×cos60°=
×1×cos60°= .
.在△CFM中,由余弦定理可得CM2=
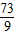 =7+
=7+ -2×
-2×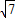 ×
×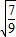 ×cos∠CFM,解得cos∠CFM=-
×cos∠CFM,解得cos∠CFM=-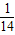 ,
,故异面直线DE与CF的夹角的余弦为
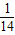 ,
,故答案为
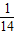 .
.点评:本题主要考查异面直线所成的角的定义和求法,余弦定理的应用,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目