题目内容
学校文艺队每个成员唱歌、跳舞至少会一门,已知会唱歌的人有5人,会跳舞的有3人.现从中任选2人,其中至少一个人既会唱歌,又会跳舞的概率为| 3 | 5 |
(1)求选出的这2人中,都是既会唱歌,又会跳舞的概率;
(2)求选出的这2人中,恰有1人既会唱歌,又会跳舞的概率.
分析:(1)设既会唱歌,又会跳舞的人为x人,由题意有1-
=
,解得x=2,故该文艺队共6人,既会唱歌又会跳舞的人有2人,根据题意可得所求的概率等于 P=
,运算得出结果.
(2)所求事件的概率为 P=
=
.
| ||
|
| 3 |
| 5 |
| ||
|
(2)所求事件的概率为 P=
| ||||
|
| 8 |
| 15 |
解答:解:(1)设既会唱歌,又会跳舞的人为x人,由题意有1-
=
,∴x=2,
∴该文艺队共6人,既会唱歌又会跳舞的人有2人.∴所求概率P=
=
.
(2)所求事件的概率为 P=
=
.
| ||
|
| 3 |
| 5 |
∴该文艺队共6人,既会唱歌又会跳舞的人有2人.∴所求概率P=
| ||
|
| 1 |
| 15 |
(2)所求事件的概率为 P=
| ||||
|
| 8 |
| 15 |
点评:本题考查等可能事件的概率,所求的事件与它的对立事件概率间的关系,求出该文艺队共6人,既会唱歌又会跳舞的人有2人,是解题的关键.

练习册系列答案
相关题目
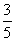 。
。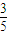 .
.