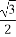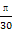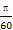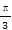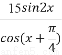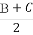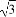题目内容

设函数f(x)=2cos2x+2sinxcosx-1(x∈R).

(1)化简函数f(x)的表达式,并求函数f(x)的最小正周期.

(2)若x∈[0,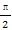],求函数f(x)的最大值与最小值.

 

(1)f(x)=2sin(2x+ T=π

(2)x=时,f(x)min=-1;x=时,f(x)max=2.

【解析】(1)∵f(x)=2cos2x+2sinxcosx-1

=cos2x+sin2x

=2sin(2x+),

∴函数f(x)的最小正周期T=π.

(2)∵0≤x≤,∴≤2x+≤,

∴-≤sin(2x+)≤1,

∴-1≤2sin(2x+)≤2,

∴当2x+=,

即x=时,f(x)min=-1;

当2x+=,

即x=时,f(x)max=2.

 

练习册系列答案
相关题目

如图,为了研究钟表与三角函数的关系,建立了如图所示的坐标系,设秒针针尖位置P(x,y).若初始位置为P0(,),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为(　　)

(A)y=sin(t+) (B)y=sin(-t-)

(C)y=sin(-t+) (D)y=sin(-t-)

 

已知圆O(O为坐标原点)的半径为1,PA,PB为该圆的两条切线,A,B为两切点,那么·的最小值为(　　)

(A)-4+(B)-3+

(C)-4+2(D)-3+2

 

已知点P为△ABC所在平面上的一点,且=+t,其中t为实数,若点P落在△ABC的内部,则t的取值范围是(　　)

(A)0<t<(B)0<t<(C)0<t<(D)0<t<

 

在以下各命题中,假命题的个数为(　　)

①“|a|=|b|”是“a=b”的必要不充分条件

②任一非零向量的方向都是唯一的

③“a∥b”是“a=b”的充分不必要条件

④若|a|-|b|=|a|+|b|,则b=0

(A)1(B)2(C)3(D)4

 

已知y=f(x)是奇函数,且图象关于x=3对称,f(1)=1,cosx-sinx=,则f()=(　　)

(A)-1 (B)0 (C)1 (D)2

 

已知关于x的方程:x2-(6+i)x+9+ai=0(a∈R)有实数根b.

(1)求实数a,b的值.

(2)若复数满足|-a-bi|-2|z|=0,求z为何值时,|z|有最小值,并求出|z|的最小值.

 

在△ABC中,角A,B,C所对的边分别为a,b,c,且cosA=.

(1)求sin2 -cos 2A的值.

(2)若a=,求bc的最大值.

 

数列{an}满足:a1=1,an+1=3an+2n+1(n∈N*),求{an}的通项公式.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网