题目内容
半径为
的圆C的圆心C在射线y=-2x(x≤0)上,且截y轴所得的弦长为1.
(1)求圆C的方程.
(2)设P为圆C上一动点,O为坐标原点,求△PCO的重心G的轨迹方程.
| ||
| 2 |
(1)求圆C的方程.
(2)设P为圆C上一动点,O为坐标原点,求△PCO的重心G的轨迹方程.
分析:(1)根据题意,假设圆心的坐标,利用点线距离,垂径定理及勾股定理,求弦长,故可求圆C的方程;
(2)设G(x,y),P(x0,y0),由重心坐标公式有:
⇒
,利用点P在圆C上,可得方程.
(2)设G(x,y),P(x0,y0),由重心坐标公式有:
|
|
解答:解:(1)因圆心C在射线y=-2x(x≤0)上,故设圆心为C(a,-2a)(a≤0),又该圆截y轴所得的弦长为1,
故由垂径定理及勾股定理知,圆心到y轴的距离为
=1,
即|a|=1,所以a=-1,从而圆C的方程为(x+1)2+(y-2)2=
.
(2)设G(x,y),P(x0,y0),由重心坐标公式有:
⇒
,又点P在圆C上,
故(x0+1)2+(y0-2)2=
,
所以有(3x+2)2+(3y-4)2=
.
又P、C、O为三角形的三顶点,
故点P在不直线y=-2x上,从而点G也不在直线y=-2x上,由
,解得
或
所以△PCO的重心G的轨迹方程为(3x+2)2+(3y-4)2=
(去除(-
,1)和(-
,
)两点).
故由垂径定理及勾股定理知,圆心到y轴的距离为
(
|
即|a|=1,所以a=-1,从而圆C的方程为(x+1)2+(y-2)2=
| 5 |
| 4 |
(2)设G(x,y),P(x0,y0),由重心坐标公式有:
|
|
故(x0+1)2+(y0-2)2=
| 5 |
| 4 |
所以有(3x+2)2+(3y-4)2=
| 5 |
| 4 |
又P、C、O为三角形的三顶点,
故点P在不直线y=-2x上,从而点G也不在直线y=-2x上,由
|
|
|
所以△PCO的重心G的轨迹方程为(3x+2)2+(3y-4)2=
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 6 |
| 5 |
| 3 |
点评:本题的考点是圆的方程的综合应用,主要考查圆的标准方程,考查代入法求轨迹方程,关键是寻找动点坐标之间的关系.

练习册系列答案
相关题目
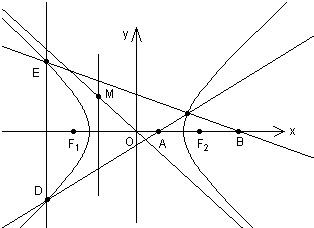 如图,双曲线
如图,双曲线