题目内容

精英家教网如图，半圆的直径AB=6，O为圆心，C为半圆上不同于A、B的任意一点，若P为半径OC上的动点，则(
PA
+
PB
)•
PC
的最小值是
 
．
分析：先利用中线的性质得
PA
+
PB
=2
PO
，再代入所求问题得（
PA
+
PB
）•
PC
=2
PO
•
PC
=-2|
PO
|•|
PC
|，利用和为定值借助于基本不等式即可求出(
PA
+
PB
)•
PC
的最小值．
解答：解：因为
PA
+
PB
=2
PO
，
∴（
PA
+
PB
）•
PC
=2
PO
•
PC
=-2|
PO
|•|
PC
|．
又因为|
PO
|+|
PC
|=|
OC
|=3≥2
|
PO|
•|
PC|
?|
PO
|•|
PC
|≤
9
4
．
所以(
PA
+
PB
)•
PC
≥-
9
2
．
故答案为：-
9
2
．
点评：本题主要考查向量在几何中的应用以及基本不等式的应用问题，是对基础知识的考查，属于基础题目．
练习册系列答案
相关题目
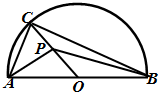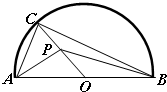精英家教网如图，半圆的直径AB=4，O为圆心，C为半圆上不同于A、B的任意一点，若P为半径OC上的动点，则(
PA
+
PB
)•
PC
的最小值是（　　）
A、2B、0C、-1D、-2
（2008•南京二模）如图，半圆的直径AB=2，O为圆心，C为半圆上不同于A，B的任意一点，若P为半径OC上的动点，则(
PA
+
PB
)•
PC
的最小值是
-
1
2
-
1
2
．
精英家教网如图，半圆的直径AB=6，O为圆心，C为半圆上不同于A、B的任意一点，若P为半径OC上的动点，则(
PA
+
PB
)•
PC
的最小值为（　　）
A、
9
2
B、9
C、-
9
2
D、-9
如图，半圆的直径AB=4，O为圆心，C是半圆上与A、B不同的任意一点，P是半径OC上的动点，则(
PA
+
PB
)•
PC
的最小值是
-2
-2
．
如图，半圆的直径AB=2，O为圆心，C是半圆上不同于A，B的任意一点，若P是半径OC上的动点．
（I）试用
OA
，
OP
表示
PA
，
PB
；
（II）若点P是OC的中点，求
PA
•
PB
的值；
（III）求（
PA
+
PB
）•
PC
的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网