题目内容
20．过点（1，2）且倾斜角α满足$\frac{sinα+cosα}{sinα-2cosα}$=-2的直线的方程为y-x-1=0．分析 由于直线的倾斜角α满足$\frac{sinα+cosα}{sinα-2cosα}$=-2，可得直线的斜率k=tanα=1．利用点斜式即可得解．
解答 解：∵直线的倾斜角α满足$\frac{sinα+cosα}{sinα-2cosα}$=$\frac{tanα+1}{tanα-2}$=-2，解得：tanα=1，
∴直线的斜率k=1．
∴直线的方程为：y-2=1（x-1），
化为y-x-1=0．
故答案为：y-x-1=0．
点评 本题主要考查了同角三角函数基本关系式，直线的点斜式方程的综合应用，属于基础题．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
8．sin4$\frac{π}{12}$-cos4$\frac{π}{12}$等于（ ）
| A． | -$\frac{1}{2}$ | B． | -$\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
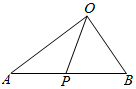如图，在△AOB中，点P在AB上，且$\overrightarrow{OP}$=m$\overrightarrow{PA}$+2m$\overrightarrow{OB}$（m∈R），求$\frac{|\overrightarrow{PA}|}{|\overrightarrow{PB}|}$的值．
12．已知集合A={y|y=（$\frac{1}{2}$）x，x≥-1}，B={y|y=ex+1，x≤0}，则下列结论正确的是（ ）
| A． | A=B | B． | A∪B=R | C． | A∩（∁RB）=∅ | D． | B∩（∁RA）=∅ |