题目内容
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,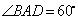 ,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3, H是CF的中点.
,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3, H是CF的中点.
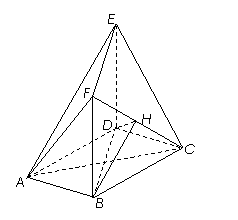 (Ⅰ)求证:AC⊥平面BDEF;
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求直线DH与平面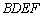 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角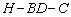 的大小.
的大小.
(Ⅰ)证明:因为四边形 是菱形,
是菱形,
所以 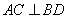 .
.
因为平面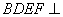 平面
平面 ,且四边形
,且四边形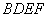 是矩形,
是矩形,
所以  平面
平面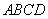 ,
,
又因为 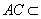 平面
平面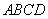 ,
,
所以 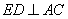 .
.
因为 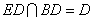 ,
,
所以 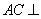 平面
平面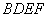 .
.
(Ⅱ)解:设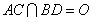 ,取
,取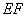 的中点
的中点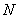 ,连接
,连接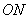 ,
,
因为四边形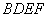 是矩形,
是矩形,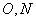 分别为
分别为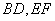 的中点,
的中点,
所以 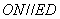 ,
,
又因为  平面
平面 ,所以
,所以 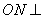 平面
平面 ,
,
由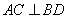 ,得
,得 两两垂直.
两两垂直.
所以以 为原点,
为原点,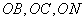 所在直线分别为x轴,y轴,z轴,如图建立空间直角坐标系.
所在直线分别为x轴,y轴,z轴,如图建立空间直角坐标系.
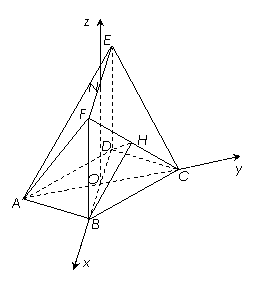 因为底面
因为底面 是边长为2的菱形,
是边长为2的菱形,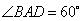 ,
,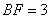 ,
,
所以 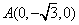 ,
,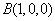 ,
,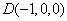 ,
,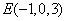 ,
,
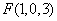 ,
,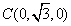 ,
,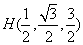 . ………………6分
. ………………6分
因为 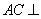 平面
平面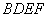 ,
,
所以平面 的法向量
的法向量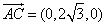 . …………7分
. …………7分
设直线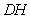 与平面
与平面 所成角为
所成角为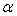 ,
,
由 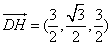 ,
,
得 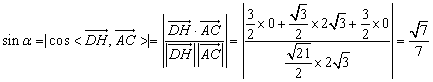 ,
,
所以直线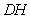 与平面
与平面 所成角的正弦值为
所成角的正弦值为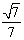 . ……
. ……
(Ⅲ)解:由(Ⅱ),得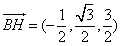 ,
,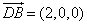 .
.
设平面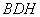 的法向量为
的法向量为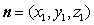 ,
,
所以
即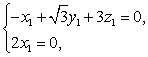
令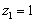 ,得
,得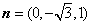 .
.
由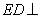 平面
平面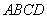 ,得平面
,得平面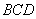 的法向量为
的法向量为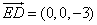 ,
,
则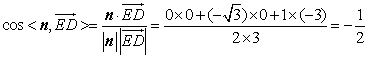 .
.
由图可知二面角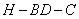 为锐角,
为锐角,
所以二面角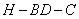 的大小为
的大小为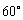 .
.

用 到
到 这
这 个数字,可以组成没有重复数字的三位偶数的个数为( )
个数字,可以组成没有重复数字的三位偶数的个数为( )
| A. | B. | C. | D. |
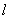 ,平面
,平面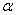 .则“
.则“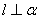 ”是“
”是“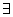 直线
直线 ,
,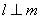 ”的 ( )
”的 ( )



 与x轴切于A点,与y轴切于B点,设劣弧
与x轴切于A点,与y轴切于B点,设劣弧 的中点为M,则过点M的圆C的切线方程是( )
的中点为M,则过点M的圆C的切线方程是( ) (B)
(B) (C)
(C) (D)
(D)
 ,
, ,那么
,那么 等于
等于 B.
B. C.
C. D.
D.
 的值为
的值为  B.
B. C.
C. D.
D.
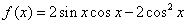 .
.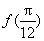 ;
;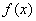 的最大值和单调递增区间.
的最大值和单调递增区间.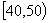 ,
,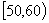 ,…,
,…,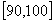 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.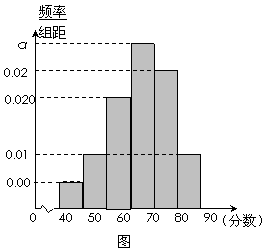 (Ⅰ)求图中实数
(Ⅰ)求图中实数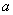 的值;
的值;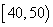 与
与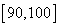 两个分
两个分