题目内容
已知函数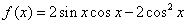 .
.
(Ⅰ)求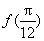 ;
;
(Ⅱ)求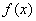 的最大值和单调递增区间.
的最大值和单调递增区间.
解: (Ⅰ)因为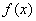
 ,
,
所以 .
.
(Ⅱ)



当 时,函数
时,函数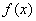 的最大值为
的最大值为 .
.
令 ,
,
得 .
.
所以函数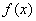 的单调递增区间是
的单调递增区间是 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
从一堆苹果中任取20粒,称得各粒苹果的质量(单位:克)数据分布如下表所示:
| 分组 |
|
|
|
|
|
|
| 频数 | 1 | 3 | 4 | 6 |
| 2 |
根据频数分布表,可以估计在这堆苹果中,质量大于130克的苹果数约占苹果总数的
A.10% B.30% C.60% D.80%
 .
. 中,
中, ,求
,求 的值;
的值; 的最小正周期及其图象的所有对称轴的方程.
的最小正周期及其图象的所有对称轴的方程. ,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3, H是CF的中点.
,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3, H是CF的中点.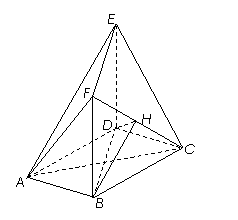 (Ⅰ)求证:AC⊥平面BDEF;
(Ⅰ)求证:AC⊥平面BDEF;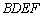 所成角的正弦值;
所成角的正弦值;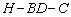 的大小.
的大小. 在
在 上的最大值是3,那么
上的最大值是3,那么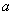 等于
等于  B.
B.  C.
C.  D.
D.
 的结果为 .
的结果为 . 且
且 命题
命题 ,命题
,命题
 ,
, 是
是 的( )
的( ) 在
在 上是单调函数,且满足对任意
上是单调函数,且满足对任意 ,都有
,都有 ,则
,则 的值是( )
的值是( )






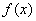 的导函数
的导函数 的图象如图所示,则函数
的图象如图所示,则函数