题目内容
已知椭圆C: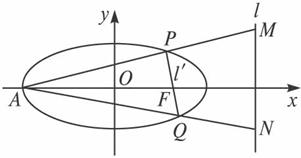
(1)求![]() 的取值范围;
的取值范围;
(2)若AP∩l=M,AQ∩l=N,求证:M、N两点的纵坐标之积为定值.
答案:(理21文22)解:(1)①当直线PQ的斜率不存在时,点P(1,![]() ),Q(1,-
),Q(1,-![]() ),A(-2,0),
),A(-2,0),
![]() =(3,
=(3,![]() ),
),![]() =(3,-
=(3,-![]() ),
),![]() =3×3-
=3×3-![]() =
=![]() .
.
②设直线PQ的斜率为k,P(x1,y1),Q(x2,y2),方程为y=k(x-1)(k≠0),

代入椭圆方程得(4k2+3)x2-8k2x+4k2-12=0.∴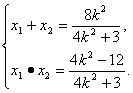
![]() =(x1+2,y1),
=(x1+2,y1),![]() =(x2+2,y2).
=(x2+2,y2).![]() =x1x2+2(x1+x2)+4+y1y2
=x1x2+2(x1+x2)+4+y1y2
=(k2+1)x1x2+(2-k2)(x1+x2)+4+k2=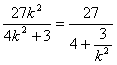 .
.
∵![]() ,∴0<
,∴0<![]() <
<![]() .综上所述,∴0<
.综上所述,∴0<![]() ≤
≤![]() .
.
(2)设M(4,y3),N(4,y4),∴y3=![]() .∴y4=
.∴y4=![]() ,
,
y3·y4=![]() =
=![]() =-9.
=-9.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
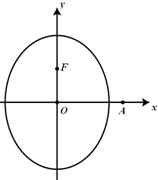 (2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=
(2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=







