题目内容
已知△ABC的三个顶点在以O为球心的球面上,且∠B=90°,BC=1,AC=3,已知三棱锥O-ABC的体积为
,则球O的表面积为 .
| ||
| 6 |
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:确定斜边AC的中点就是△ABC的外接圆的圆心,利用三棱锥O-ABC的体积,求出O到底面的距离,即可求出球的半径,然后求出球的表面积.
解答:
解:∵△ABC的三个顶点在以O为球心的球面上,且∠B=90°,BC=1,AC=3,
∴斜边AC的中点就是△ABC的外接圆的圆心,
∵三棱锥O-ABC的体积为
,AB=2
,
∴
×
×2
×1×h=
,
∴h=
,
∴R=
=2,
∴球O的表面积为4πR2=16π.
故答案为:16π.
∴斜边AC的中点就是△ABC的外接圆的圆心,
∵三棱锥O-ABC的体积为
| ||
| 6 |
| 2 |
∴
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| ||
| 6 |
∴h=
| ||
| 2 |
∴R=
(
|
∴球O的表面积为4πR2=16π.
故答案为:16π.
点评:本题考查球的表面积的求法,球的内含体与三棱锥的关系,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
已知双曲线
-
=1的一条渐近线方程为y=
x,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
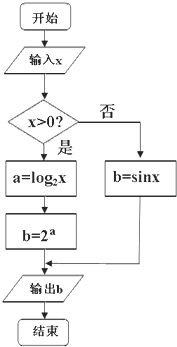 如图所示的程序框图,若两次输入的x值分别是3π和-
如图所示的程序框图,若两次输入的x值分别是3π和-| π |
| 3 |
A、1,
| ||||
B、0,
| ||||
C、-π,-
| ||||
D、3π,-
|
下列函数中,二次函数是( )
| A、y=8x2+1 | ||
| B、y=8x+1 | ||
C、y=
| ||
D、y=
|
若集合M={a,b,c},N={x|x⊆M},则下列关系正确的是( )
| A、M∈N | B、N⊆M |
| C、M⊆N | D、M=N |
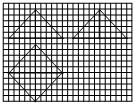 一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为
一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为