题目内容
已知双曲线
-
=1的一条渐近线方程为y=
x,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由双曲线
-
=1的一条渐近线方程为y=
x,推出b、a的关系式,由此能求出该双曲线的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
解答:
解:∵双曲线
-
=1的一条渐近线方程为y=
x,
∴4a=3b,
∴c=
=
a
∴e=
=
.
故选:B.
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
∴4a=3b,
∴c=
| a2+b2 |
| 5 |
| 3 |
∴e=
| c |
| a |
| 5 |
| 3 |
故选:B.
点评:本题考查双曲线的离心率的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在平面直角坐标系中,不等式组
,(a是常数)表示的平面区域面积是9,那么实数a的值为( )
|
A、3
| ||
B、-3
| ||
| C、-5 | ||
| D、1 |
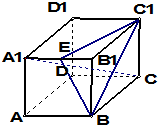 在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,
在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,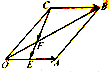 如图,在平行四边形OABC中,E是OA的中点,F在对角线OB上,且OF=
如图,在平行四边形OABC中,E是OA的中点,F在对角线OB上,且OF=