题目内容
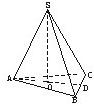 若正三棱锥底面边长为4,体积为1,则侧面和底面所成二面角的大小等于
若正三棱锥底面边长为4,体积为1,则侧面和底面所成二面角的大小等于分析:二面角的度量关键在于找出它的平面角,构造平面角常用的方法就是三垂线法.取BC的中点D,连接SD、AD,则SD⊥BC,AD⊥BC,所以∠SDA为侧面与底面所成二面角的平面角.在平面SAD中,作SO⊥AD与AD交于O,则SO为棱锥的高,大小可由体积求得.
解答:解:取BC的中点D,连接SD、AD,则SD⊥BC,AD⊥BC.
∴∠SDA为侧面与底面所成二面角的平面角,设为α.
在平面SAD中,作SO⊥AD与AD交于O,则SO为棱锥的高.
AO=2DO,∴OD=
.
又VS-ABC=
•
AB•BC•sin60°•h=1,
∴h=
.∴tanα=
=
=
.
∴α=arctan
.
∴∠SDA为侧面与底面所成二面角的平面角,设为α.
在平面SAD中,作SO⊥AD与AD交于O,则SO为棱锥的高.
AO=2DO,∴OD=
| 2 |
| 3 |
| 3 |
又VS-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
∴h=
| ||
| 4 |
| SO |
| DO |
| ||||
|
| 3 |
| 8 |
∴α=arctan
| 3 |
| 8 |
点评:本小题主要考查空间线面关系、二面角的度量等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

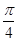 ,则其体积为____________。
,则其体积为____________。