题目内容
【题目】已知向量 ![]() =(cosx,﹣
=(cosx,﹣ ![]() ),
), ![]() =(
=( ![]() sinx,cos2x),x∈R,设函数f(x)=
sinx,cos2x),x∈R,设函数f(x)= ![]() .
.
(1)求f(x)的最小正周期.
(2)求f(x)在[0, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
【答案】
(1)解:函数f(x)= ![]() =(cosx,﹣
=(cosx,﹣ ![]() )(
)( ![]() sinx,cos2x)
sinx,cos2x)
= ![]() sinxcosx
sinxcosx ![]()
=sin(2x﹣ ![]() )
)
最小正周期为:T= ![]() =π.
=π.
(2)解:当x∈[0, ![]() ]时,2x﹣
]时,2x﹣ ![]() ∈
∈ ![]() ,
,
由正弦函数y=sinx在 ![]() 的性质可知,sinx
的性质可知,sinx ![]() ,
,
∴sin(2x﹣ ![]() )
) ![]() ,
,
∴f(x)∈[﹣ ![]() ,1],
,1],
所以函数f(x)在[0, ![]() ]上的最大值和最小值分别为:1,﹣
]上的最大值和最小值分别为:1,﹣ ![]() .
.
【解析】(1)通过向量的数量积以及二倍角的正弦函数两角和的正弦函数,化简函数为一个角的一个三角函数的形式,通过周期公式,求f(x)的最小正周期.(2)通过x在[0, ![]() ],求出f(x)的相位的范围,利用正弦函数的最值求解所求函数的最大值和最小值.
],求出f(x)的相位的范围,利用正弦函数的最值求解所求函数的最大值和最小值.
【考点精析】本题主要考查了两角和与差的正弦公式和三角函数的最值的相关知识点,需要掌握两角和与差的正弦公式:![]() ;函数
;函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.

【题目】在2016年6月英国“脱欧”公投前夕,为了统计该国公民是否有“留欧”意愿,该国某中学数学兴趣小组随机抽查了50名不同年龄层次的公民,调查统计他们是赞成“留欧”还是反对“留欧”.现已得知50人中赞成“留欧”的占60%,统计情况如下表:
年龄层次 | 赞成“留欧” | 反对“留欧” | 合计 |
18岁—19岁 | 6 | ||
50岁及50岁以上 | 10 | ||
合计 | 50 |
(1)请补充完整上述列联表;
(2)请问是否有97.5%的把握认为赞成“留欧”与年龄层次有关?请说明理由.
参考公式与数据: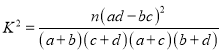 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

