题目内容
已知f(x)=ex+x2-x;
(1)求f(x)的单调区间;
(2)若g(x)与f(x)的图象关于y轴对称,写出g(x)的表达式,并比较g(x)与f(x)的大小;
(3)若f(x1)=f(x2),求证:x1+x2<0.
(1)求f(x)的单调区间;
(2)若g(x)与f(x)的图象关于y轴对称,写出g(x)的表达式,并比较g(x)与f(x)的大小;
(3)若f(x1)=f(x2),求证:x1+x2<0.
考点:利用导数研究函数的单调性,函数的图象与图象变化
专题:函数的性质及应用,导数的综合应用
分析:(1)利用导数求函数的单调性,利用二次求导求导函数的符号,(2)函数y=f(x)与函数y=g(x)的图象关于x轴对称,则有g(x)=-f(x),(3)先由(1)得f(x)在(0,+∞)内是增函数,在(-∞,0)内是减函数,故x1、x2不可能在同一单调区间内;设x1<0<x2,令g(x)=f(x)-f(-x),由函数g(x)的单调性,即g(x1)<g(0)=0.再结合函数的单调性即可证明结论.
解答:
解:(1)∵f(x)=ex+x2-x,
∴f′(x)=ex+2x-1,f″(x)=ex+2>0,
∴f′(x)=ex+2x-1为单调增函数
令f′(x)=0,可得x=0
当x<0时,f′(x)<0,函数f(x)单调减,当x>0时,f′(x)>0,函数f(x)单调增,
所以函数的单调减区间为(-∞,0],增区间为(0,+∞).
(2)若g(x)与f(x)的图象关于y轴对称,则g(x)=-f(x)=-ex-x2+x,
做差得f(x)-g(x)=2(ex+x2-x)=2f(x),
令F(x)=2f(x),由(1)可知F(x)与f(x)一样在(-∞,0],单调递减,在(0,+∞).单调递增,x=0时取得最小值F(0)=1,
所以f(x)-g(x)>0,即g(x)<f(x).
(3)证明:)∵f(x1)=f(x2),且满足x1≠x2,由(1)可知x1,x2异号.
不妨设x1<0<x2,则-x1>0.
令g(x)=f(x)-f(-x)=ex+x2-x-(e-x+x2+x)
=ex-e-x-2x,
则g′(x)=ex+e-x-2≥2
-2=0,
所以g(x)在R上是增函数,
又g(x1)=f(x1)-f(-x1)<g(0)=0,∴f(x2)=f(x1)<f(-x1),
又∵f(x)在(0,+∞)上是增函数,
∴x2<-x1,即x1+x2<0.
∴f′(x)=ex+2x-1,f″(x)=ex+2>0,
∴f′(x)=ex+2x-1为单调增函数
令f′(x)=0,可得x=0
当x<0时,f′(x)<0,函数f(x)单调减,当x>0时,f′(x)>0,函数f(x)单调增,
所以函数的单调减区间为(-∞,0],增区间为(0,+∞).
(2)若g(x)与f(x)的图象关于y轴对称,则g(x)=-f(x)=-ex-x2+x,
做差得f(x)-g(x)=2(ex+x2-x)=2f(x),
令F(x)=2f(x),由(1)可知F(x)与f(x)一样在(-∞,0],单调递减,在(0,+∞).单调递增,x=0时取得最小值F(0)=1,
所以f(x)-g(x)>0,即g(x)<f(x).
(3)证明:)∵f(x1)=f(x2),且满足x1≠x2,由(1)可知x1,x2异号.
不妨设x1<0<x2,则-x1>0.
令g(x)=f(x)-f(-x)=ex+x2-x-(e-x+x2+x)
=ex-e-x-2x,
则g′(x)=ex+e-x-2≥2
| exe-x |
所以g(x)在R上是增函数,
又g(x1)=f(x1)-f(-x1)<g(0)=0,∴f(x2)=f(x1)<f(-x1),
又∵f(x)在(0,+∞)上是增函数,
∴x2<-x1,即x1+x2<0.
点评:本题考查了利用导数研究函数的单调性极值与最值、恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知函数f(x)=(2x-x2)ex,则( )
A、f(
| ||
B、f(
| ||
C、f(-
| ||
| D、f(x)没有最大值也没有最小值 |
设函数f(x)=x3-2ex2+mx-lnx,记g(x)=
,若函数g(x)至少存在一个零点,则实数m的取值范围是( )
| f(x) |
| x |
A、(-∞,e2+
| ||||
B、(0,e2+
| ||||
C、(e2+
| ||||
D、(-e2-
|
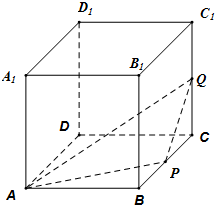 正方体ABCD-A1B1C1D1为棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是
正方体ABCD-A1B1C1D1为棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是