题目内容
已知函数f(x)=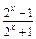 (x∈R),
(x∈R),
(1)判定函数f(x)的奇偶性;
(2)判定函数f(x)在R上的单调性,并证明.
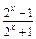 (x∈R),
(x∈R),(1)判定函数f(x)的奇偶性;
(2)判定函数f(x)在R上的单调性,并证明.
(1)f(x)是奇函数(2)f(x)在R上单调递增
(1)对 x∈R有-x∈R,
x∈R有-x∈R,
并且f(-x)= =
= =-
=-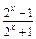 =-f(x),
=-f(x),
所以f(x)是奇函数.
(2)f(x)在R上单调递增,证明如下:
任取x1,x2∈R,并且x1>x2,
f(x1)-f(x2)= -
-
=
= .
.
∵x1>x2,∴ >
> >0,
>0,
∴ -
- >0,
>0,  +1>0,
+1>0,  +1>0.
+1>0.
∴ >0.
>0.
∴f(x1)>f(x2).
∴f(x)在R上为单调递增函数.
 x∈R有-x∈R,
x∈R有-x∈R,并且f(-x)=
 =
= =-
=-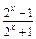 =-f(x),
=-f(x),所以f(x)是奇函数.
(2)f(x)在R上单调递增,证明如下:
任取x1,x2∈R,并且x1>x2,
f(x1)-f(x2)=
 -
-
=

=
 .
.∵x1>x2,∴
 >
> >0,
>0,∴
 -
- >0,
>0,  +1>0,
+1>0,  +1>0.
+1>0.∴
 >0.
>0.∴f(x1)>f(x2).
∴f(x)在R上为单调递增函数.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 求证:
求证:
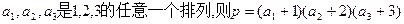 必是偶数.
必是偶数.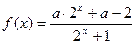 为奇函数.
为奇函数.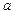 的值;
的值;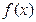 在其定义域上为增函数
在其定义域上为增函数 ,证明方程
,证明方程 没有负数根
没有负数根 .
.