题目内容
 如图所示,空间直角坐标系中,直三棱柱ABC-A′B′C′,AB=BC=2,BB′=2,N、M分别是A′C′、B′C′的中点.
如图所示,空间直角坐标系中,直三棱柱ABC-A′B′C′,AB=BC=2,BB′=2,N、M分别是A′C′、B′C′的中点.(1)试画出该直三棱柱ABC-A′B′C′的侧视图.并标注出相应线段长度值;
(2)求证:直线AN与BM相交,并求二面角M-AN-C的余弦值.
分析:(1)要画直三棱柱的侧视图,我们可以直观图可得,B为直角,侧面是一个边长为2的正方形.
(2)要证明AN和BM相交,我们可以结合公理3,证明三线共点,要求二面角M-AN-C的余弦值,我们可以A为坐标原点,AB,AC,AA',为坐标轴建立空间坐标系,利用空间向量求解.
(2)要证明AN和BM相交,我们可以结合公理3,证明三线共点,要求二面角M-AN-C的余弦值,我们可以A为坐标原点,AB,AC,AA',为坐标轴建立空间坐标系,利用空间向量求解.
解答:解:(1)直三棱柱ABC-A′B′C′的侧视图如下图示:

(2)证明:如下图所示:

∵由MN∥A'B',MN=
A'B',
∴MN∥AB,MN=
AB,
则四边形AMNB为梯形.
令AM∩BN=P,
则P∈AM,而AM?平面ACC'A',P∈BN,BN?平面ACC'A',
平面ACC'A'∩平面ACC'A'=CC',∴P∈CC'.
∴直线AN与BM相交.
以A为坐标原点,AB,AC,AA',为坐标轴建立空间坐标系,
则易得:平面MAN的一个法向量为
=(2,0,-1),
平面CAN的一个法向量为
=B′
(1,1,0),
,
=
=
故二面角M-AN-C的余弦值
.

(2)证明:如下图所示:

∵由MN∥A'B',MN=
| 1 |
| 2 |
∴MN∥AB,MN=
| 1 |
| 2 |
则四边形AMNB为梯形.
令AM∩BN=P,
则P∈AM,而AM?平面ACC'A',P∈BN,BN?平面ACC'A',
平面ACC'A'∩平面ACC'A'=CC',∴P∈CC'.
∴直线AN与BM相交.
以A为坐标原点,AB,AC,AA',为坐标轴建立空间坐标系,
则易得:平面MAN的一个法向量为
| n |
平面CAN的一个法向量为
| m |
| N= |
| m |
| n |
| 2 | ||||
|
| ||
| 5 |
故二面角M-AN-C的余弦值
| ||
| 5 |
点评:空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值;
空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;
空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值;
空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;
空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
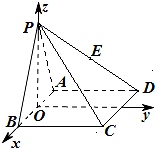 如图,△PAB是正三角形,四边形ABCD是正方形,
如图,△PAB是正三角形,四边形ABCD是正方形,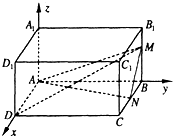 已知在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=3,M,N分别是棱BB1,BC上的点,且BM=2,BN=1,建立如图所示的空间直角坐标系.求:
已知在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=3,M,N分别是棱BB1,BC上的点,且BM=2,BN=1,建立如图所示的空间直角坐标系.求: 在如图所示的空间直角坐标系中,AB=AD=2,AC=4,E,F分别是AD,BD的中点.
在如图所示的空间直角坐标系中,AB=AD=2,AC=4,E,F分别是AD,BD的中点. 如图所示的空间直角坐标系A-xyz中,正三角形△ABC中AB=2,AA1∥BB1∥CC1,AA1=BB1=CC1=2,D,E分别为A1C,BB1的中点.
如图所示的空间直角坐标系A-xyz中,正三角形△ABC中AB=2,AA1∥BB1∥CC1,AA1=BB1=CC1=2,D,E分别为A1C,BB1的中点.