题目内容
如图所示的空间直角坐标系A-xyz中，正三角形△ABC中AB=2，AA1∥BB1∥CC1，AA1=BB1=CC1=2，D，E分别为A1C，BB1的中点．（Ⅰ）求证：DE∥平面ABC；
（Ⅱ）求异面直线BD与CE所成角的大小．
分析：在空间直角坐标系中，先确定相关点的坐标，（1）取取AC的中点F，利用向量证明DE∥BF，从而由线面平行的判定定理得证（2）分别求出两条异面直线的方向向量的坐标，再利用向量数量积运算的夹角公式计算向量夹角的余弦值，最后由异面直线所成的角的范围得角的大小
解答：解：依题意，A（0，0，0），B（
，1，0），C（0，2，0），D（0，1，1），E（
，1，1）
（1）取AC的中点F（0，1，0），则
=（-
，0，0），
=（-
，0，0）
∴
=
∴DE∥BF
又BF?平面ABC，DE?平面ABC
∴DE∥平面ABC
（2）∵
=（-
，0，1），
=（
，-1，1）
∴cos＜
，
＞=
=
=-
∴异面直线BD与CE所成角的余弦值为
∴异面直线BD与CE所成角的大小为arccos
| 3 |
| 3 |
（1）取AC的中点F（0，1，0），则
| BF |
| 3 |
| ED |
| 3 |
∴
| BF |
| ED |
∴DE∥BF
又BF?平面ABC，DE?平面ABC
∴DE∥平面ABC
（2）∵
| BD |
| 3 |
| CE |
| 3 |
∴cos＜
| BD |
| CE |
| ||||
|
|
| -3+0+1 | ||||
|
| ||
| 5 |
∴异面直线BD与CE所成角的余弦值为
| ||
| 5 |
∴异面直线BD与CE所成角的大小为arccos
| ||
| 5 |
点评：本题综合考查了空间直角坐标系的方法解决立体几何问题，线面平行的判定定理，求异面直线所成的角的方法
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
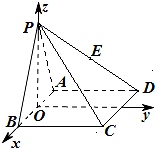如图，△PAB是正三角形，四边形ABCD是正方形，
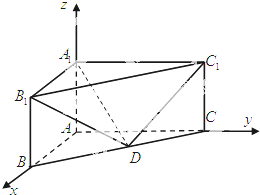三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中，已知AB=2，AC=4，AA1=3．D是BC的中点．
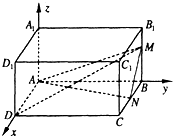已知在长方体ABCD-A1B1C1D1中，AB=4，AD=2，AA1=3，M，N分别是棱BB1，BC上的点，且BM=2，BN=1，建立如图所示的空间直角坐标系．求：
在如图所示的空间直角坐标系中，AB=AD=2，AC=4，E，F分别是AD，BD的中点．
已知正三棱柱ABC-A1B1C1，底面边长AB=2，AB1⊥BC1，点O、O1分别是边AC，A1C1的中点，建立如图所示的空间直角坐标系．