题目内容
椭圆C1: =1(a>b>0)的左右顶点分别为A、B.点P双曲线C2:
=1(a>b>0)的左右顶点分别为A、B.点P双曲线C2: =1在第一象限内的图象上一点,直线AP、BP与椭圆C1分别交于C、D点.若△ACD与△PCD的面积相等.
=1在第一象限内的图象上一点,直线AP、BP与椭圆C1分别交于C、D点.若△ACD与△PCD的面积相等.
(1)求P点的坐标;
(2)能否使直线CD过椭圆C1的右焦点,若能,求出此时双曲线C2的离心率,若不能,请说明理由.
解:(1)设P(x0,y0)(x0>0,y0>0),又有点A(-a,0),B(a,0).
∵S△ACD=S△PCD,
∴C为AP的中点,∴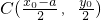 .
.
将C点坐标代入椭圆方程,得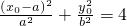 ,
,
又
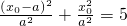 ,
,
∴x0=2a(x0=-a舍去),
∴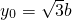 ,
,
∴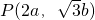 .
.
(2)∵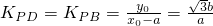 ,
,
直线PD: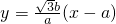 代入
代入 ?2x2-3ax+a2=0
?2x2-3ax+a2=0
∴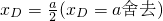 ,
,
∴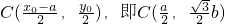
∴CD垂直于x轴.若CD过椭圆C1的右焦点,则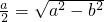 ,
,
∴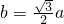 ,
,
∴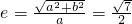 .故可使CD过椭圆C1的右焦点,此时C2的离心率为
.故可使CD过椭圆C1的右焦点,此时C2的离心率为 .
.
分析:(1)设P(x0,y0)(x0>0,y0>0),又有点A(-a,0),B(a,0).由S△ACD=S△PCD,知C为AP的中点,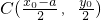 .将C点坐标代入椭圆方程,得
.将C点坐标代入椭圆方程,得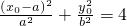 ,由此能够推导出
,由此能够推导出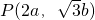 .
.
(2)由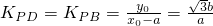 ,把直线PD:
,把直线PD: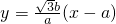 代入
代入 ?2x2-3ax+a2=0.由此入手能够导出可使CD过椭圆C1的右焦点,此时C2的离心率为
?2x2-3ax+a2=0.由此入手能够导出可使CD过椭圆C1的右焦点,此时C2的离心率为 .
.
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,注意合理地进行等价转化.
∵S△ACD=S△PCD,
∴C为AP的中点,∴
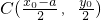 .
.将C点坐标代入椭圆方程,得
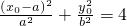 ,
,又

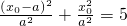 ,
,∴x0=2a(x0=-a舍去),
∴
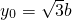 ,
,∴
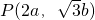 .
.(2)∵
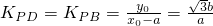 ,
,直线PD:
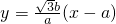 代入
代入 ?2x2-3ax+a2=0
?2x2-3ax+a2=0∴
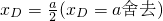 ,
,∴
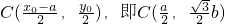
∴CD垂直于x轴.若CD过椭圆C1的右焦点,则
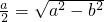 ,
,∴
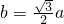 ,
,∴
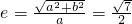 .故可使CD过椭圆C1的右焦点,此时C2的离心率为
.故可使CD过椭圆C1的右焦点,此时C2的离心率为 .
.分析:(1)设P(x0,y0)(x0>0,y0>0),又有点A(-a,0),B(a,0).由S△ACD=S△PCD,知C为AP的中点,
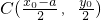 .将C点坐标代入椭圆方程,得
.将C点坐标代入椭圆方程,得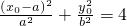 ,由此能够推导出
,由此能够推导出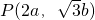 .
.(2)由
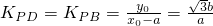 ,把直线PD:
,把直线PD: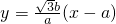 代入
代入 ?2x2-3ax+a2=0.由此入手能够导出可使CD过椭圆C1的右焦点,此时C2的离心率为
?2x2-3ax+a2=0.由此入手能够导出可使CD过椭圆C1的右焦点,此时C2的离心率为 .
.点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
相关题目
 ="1" (a>b>0)的左、右焦点分别为F1、F2, F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
="1" (a>b>0)的左、右焦点分别为F1、F2, F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|= .
.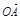 ·
· =0,求直线l的方程.
=0,求直线l的方程. +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,直线l:x-y+
,直线l:x-y+ =0与椭圆C1相切.
=0与椭圆C1相切. +
+ =1(a、b>0)焦点为顶点,以椭圆C1的顶点为焦点的双曲线C2,下列结论中错误的是( )
=1(a、b>0)焦点为顶点,以椭圆C1的顶点为焦点的双曲线C2,下列结论中错误的是( ) =1
=1