题目内容
以椭圆C1：
+
=1（a、b＞0）焦点为顶点，以椭圆C1的顶点为焦点的双曲线C2，下列结论中错误的是（ ）A．C2的方程为
=1B．C1、C2的离心率的和是1
C．C1、C2的离心率的积是1
D．短轴长等于虚轴长
【答案】分析：依题意，可求得双曲线C2的方程，从而利用双曲线的性质可对A，B，C，D四个选项逐一分析．
解答：解：依题意，双曲线C2的焦点在x轴，半焦距为a，实半轴长为
，虚半轴为b，
∴双曲线C2的方程为：
-
=1，故A正确，D正确；
对于椭圆C1：其离心率e1=
，
对于双曲线C2，其离心率e2=
，
∵e1•e2=1，故C正确；
而e1+e2≠1，故B错误．
综上所述，错误的是B．
故选B．
点评：本题考查椭圆与双曲线的简单性质，求得双曲线C2的方程是关键，考查推理、分析与运算的能力，属于中档题．
解答：解：依题意，双曲线C2的焦点在x轴，半焦距为a，实半轴长为
，虚半轴为b，∴双曲线C2的方程为：
-=1，故A正确，D正确；对于椭圆C1：其离心率e1=
，对于双曲线C2，其离心率e2=
，∵e1•e2=1，故C正确；
而e1+e2≠1，故B错误．
综上所述，错误的是B．
故选B．
点评：本题考查椭圆与双曲线的简单性质，求得双曲线C2的方程是关键，考查推理、分析与运算的能力，属于中档题．
练习册系列答案
相关题目
+
=1（a、b＞0）焦点为顶点，以椭圆C1的顶点为焦点的双曲线C2，下列结论中错误的是
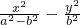=1